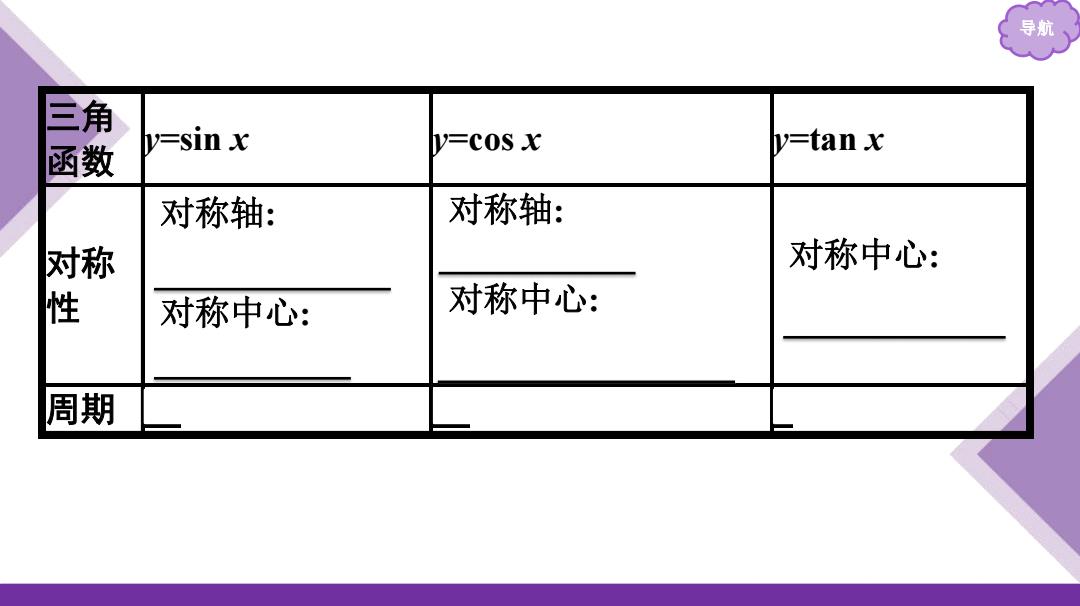
导航、 三角 函数 y=sin x V-cOS x y=tan x 对称轴: 对称轴: 对称 对称中心: 性 对称中心: 对称中心: 周期
导航 三角 函数 y=sin x y=cos x y=tan x 对称 性 对称轴: x=kπ+ 𝛑 𝟐 (k∈Z) 对称中心: (kπ,0)(k∈Z) 对称轴: x=kπ(k∈Z) 对称中心: 𝒌𝛑 + 𝛑 𝟐 ,𝟎 (k∈Z) 对称中心: 𝒌𝛑 𝟐 ,𝟎 (k∈Z) 周期 2π 2π π

导航 三角 函数 v=sinx V=cos x v=tan x 单调增区间: 单调增区间: 单调增区 单调 间: 性 单调减区间: 单调减区间: 奇偶 性
导航 三角 函数 y=sin x y=cos x y=tan x 单调 性 单调增区间: [2kπ- 𝛑 𝟐 ,2kπ+ 𝛑 𝟐 ](k∈Z) 单调减区间: [2kπ+ 𝛑 𝟐 ,2kπ+ 𝟑𝛑 𝟐 ](k∈Z) 单调增区间: [2kπ-π,2kπ](k∈Z) 单调减区间: [2kπ,2kπ+π](k∈Z) 单调增区 间: (kπ- 𝛑 𝟐 ,kπ+ 𝛑 𝟐 ) (k∈Z) 奇偶 性 奇 偶 奇

导航 10.用“五点法”画y=Asin(wx+p)一个周期的简图时,如何列表? 提示: p 3 n-p p 2π-0 0 0 0 0 π 3π @x+o 0 2 元 2 2π =Asin(@x+0) 0 A 0 A 0
导航 10.用“五点法”画y=Asin(ωx+φ)一个周期的简图时,如何列表? 提示: x - 𝛗 𝛚 𝝅 𝟐 -𝛗 𝛚 𝝅-𝛗 𝛚 𝟑𝝅 𝟐 -𝛗 𝛚 𝟐𝝅-𝛗 𝛚 ωx+φ 0 𝝅 𝟐 π 𝟑𝝅 𝟐 2π y=Asin(ωx+φ) 0 A 0 -A 0
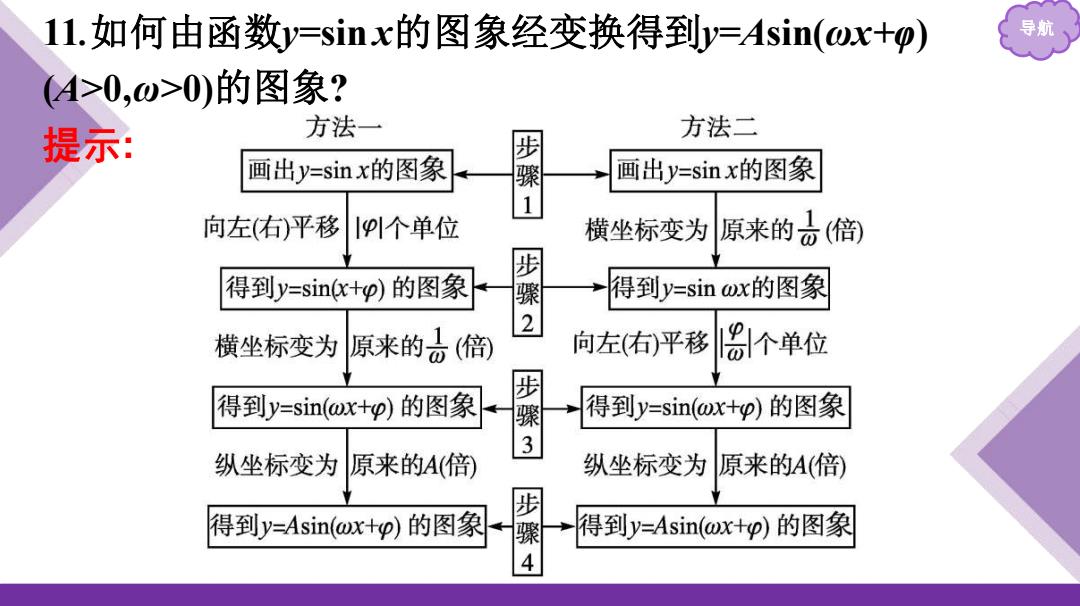
1L.如何由函数y=sinx的图象经变换得到y=Asin(ox+p) 导航 (A>0,w>0)的图象? 提示: 方法一 方法二 步 画出y=sinx的图象 画出y=sinx的图象 向左(右)平移p个单位 横坐标变为 原来的六(倍) 步 得到y=sinc+p)的图象 得到y=sin x的图象 2 横坐标变为 原来的倍) 向左(右)平移 1个单位 得到y=sin(ox+p)的图象 步 得到y=sin(wx+p)的图象 3 纵坐标变为 原来的A(倍) 纵坐标变为 原来的A(倍) 步 得到y=Asin(ox+p)的图象 得到y=Asin(ox+p)的图象 4
导航 11.如何由函数y=sin x的图象经变换得到y=Asin(ωx+φ) (A>0,ω>0)的图象? 提示: