
重点:二重积分的计算方法 难点:区域的正确划分 关键:区域的表示方法 相关基础和识:定积分的计算、 图形的投影变换 2012329 素山医学院信息工程学院高等数学教研室

第十章重积分 第一节二重积分的概念与性质 第二节二重积分的计算法 第三节三重积分 第四节重积分的应用 第五节含参变量的积分 2012329 泰山医学院信息工程学院高等数学教研室

第二节二重积分的计算法 一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、二重积分的换元法 四、小结 2012329 泰山医学院信息工程学院高等数学教研室 33

“、 利用直角坐标计算二重积分 如果积分区域为:a≤x≤b,p,(x)≤y≤P(x): [X一型] y=:(x) y=0(x) D y=o(x) 其中函数p,(x)、p,(x)在区间[a,b]上连续. 2012329 泰山医学院信息工程学院高等数学教研室
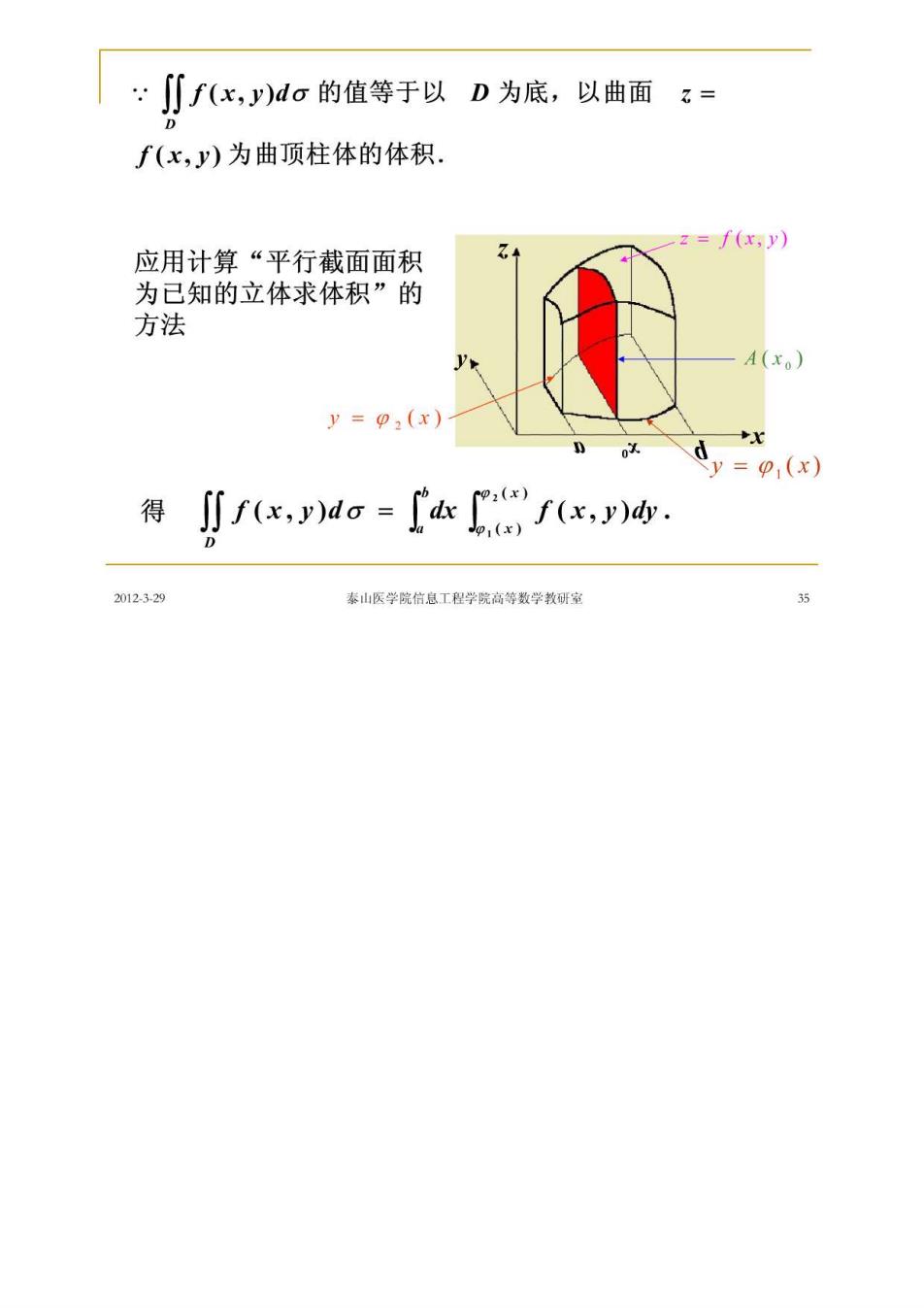
~∬f(x,y)c的值等于以D为底,以曲面:= f(x,y)为曲顶柱体的体积。 z=f(x,y) 应用计算“平行截面面积 为已知的立体求体积”的 方法 y=9,(x) dy=0(x) 得 ∬rx,Jaa=r. 2012329 泰山医学院信息工程学院高等数学教研室