dl福a:走私船速度21)当r="<1时,2b:缉私艇速度bvc1+1Uaex o0craexu+231+r8c0白0bcVcrcr把x=0代入,得ya2(b-aa(1由题设c=3千米,取a=0.4千米/分钟并分别取b=2.0.8.0.5千米/分钟,绘制a=0.4,b= 0.5缉私挺追赶曲线,并计算得追赶时间a=0.4.b=0.8分别为:t=1.5625,5,16.667(分钟)r=0.8a=0.4,b=2可见:当走私船的速度固定不变时=0.5缉私艇的速度b越大,追赶越快,追赶r=0.2花费的时间越短,这与实际是相符的。0.51.522.501
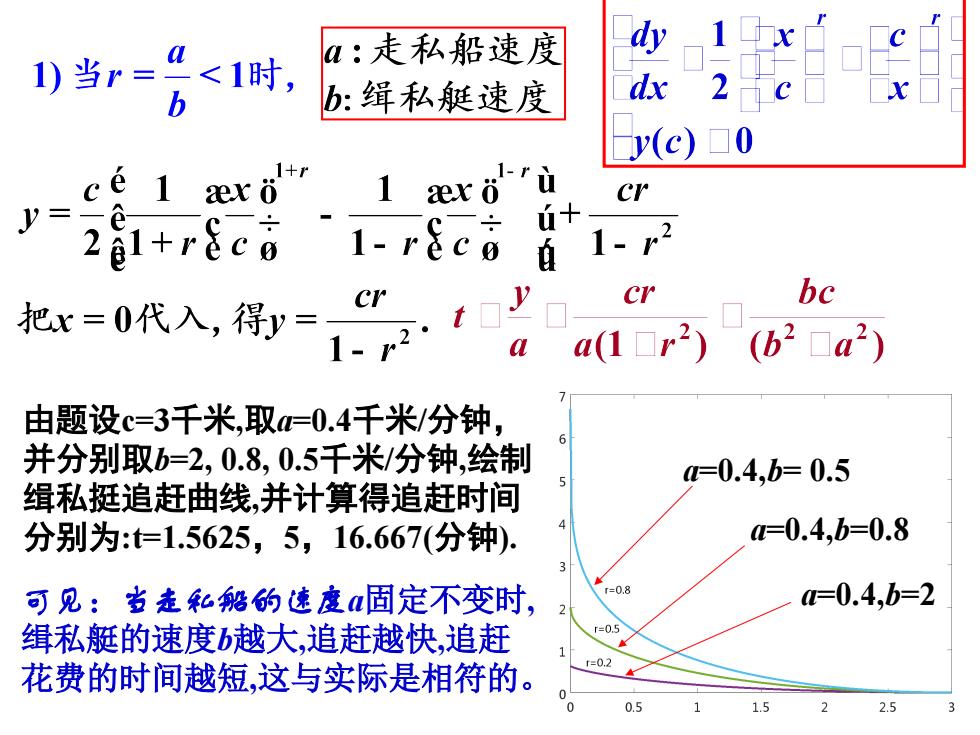
由题设c=3千米,取a=0.4千米/分钟, 并分别取b=2, 0.8, 0.5千米/分钟,绘制 缉私挺追赶曲线,并计算得追赶时间 分别为:t=1.5625,5,16.667(分钟). 可见:当走私船的速度a固定不变时, 缉私艇的速度b越大,追赶越快,追赶 花费的时间越短,这与实际是相符的。 a=0.4,b=2 a=0.4,b=0.8 a=0.4,b= 0.5

éer odyaec a:走私船速度2)当r=">1时,ec-dxb:缉私挺速度exoseC0b0y(c)1+UcrCaer oaecu2+rlexoéct0当x?0时,?+,缉私艇不可能追赶上走私船。22xo1 aex3)当r=1时,clnceeV212cC0当x0时,J?+,缉私艇不可能追赶上走私船。容易验证,模型结论与事实相符
当 时, ,缉私艇不可能追赶上走私船。 当 时, ,缉私艇不可能追赶上走私船。 容易验证,模型结论与事实相符

(2)用MATLAB软件求解析解MATLAB软件提供的解常微分方程及方程组解析解的指令是dsolve。可以用于求解存在解析解的常(组)。调用格式如下:微分方程S = dsolve(eqn)S = dsolve(eqn,cond)[yl,...,yN] = dsolve(求微分方程y=X+Xy的通解例1程序:运行结果:syms y(x)y=eqn = diff(y,x) == x+x*y;C1*exp(x^2/2) - 1y=dsolve(eqn)
(2)用MATLAB软件求解析解 MATLAB软件提供的解常微分方程及方程组解析 解的指令是dsolve,可以用于求解存在解析解的常 微分方程(组)。调用格式如下: S = dsolve(eqn) S = dsolve(eqn,cond) [y1,.,yN] = dsolve(_) 例1 求微分方程 的通解 程序: syms y(x) eqn = diff(y,x) == x+x*y; y=dsolve(eqn) 运行结果: y = C1*exp(x^2/2) – 1