
当az=1时,称a为单位向量, 如果α≠0,有长度的概念得1 a就是一个单位向量 用非零数 去乘以向量a得到一个与a同方向的 单位向量,通常称为把向量单位化
当 1时,称 为单位向量. 1 0, . 如果 有长度的概念得 就是一个单位向量 1 . 用非零数 去乘以向量 得到一个与 同方向的 单位向量,通常称为把向量 单位化

三、正交向量组的概念及求法 1.当,B]=0,称向量,B正交 说明:零向量与任意一个向量正交,并且只有零向量 与其自身正交。 定义5.1.3一组两两正交的非零向量称为正交向量组。 若正交向量组中每个向量都是单位向量,则称该向量组 为标准正交向量组. 说明:标准正交向量组也是正交向量组. 定理5.1.1正交向量组是线性无关向量组
三、正交向量组的概念及求法 1.当, 0,称向量,正交. 与其自身正交。 说明:零向量与任意一个向量正交,并且只有零向量 定义5.1.3 一组两两正交的非零向量称为正交向量组。 若正交向量组中每个向量都是单位向量,则称该向量组 为标准正交向量组. 定理5.1.1 正交向量组是线性无关向量组. 说明:标准正交向量组也是正交向量组

证明设有a1,a2,anm是正交向量组,若有 k1c1+k2C2+.+knm&m=0 用α,与等式两边做内积,得 k[a,a]=0i=1,2,.,m 由a≠0,有[a,a,>0,从而得 k=0i=1,2,.,m. 故c1,C2,.,Cm线性无关
证明 1 1 2 2 0 m m k k k , i 用a 与等式两边做内积 得 1 2 , , , 设有 m 是正交向量组,若有 [ , ] 0 1,2, , i i i k i m 0, [ , ] 0, 由i 有 i i 从而得 0 1, 2, , . i k i m 1 2 , , , . 故 m线性无关
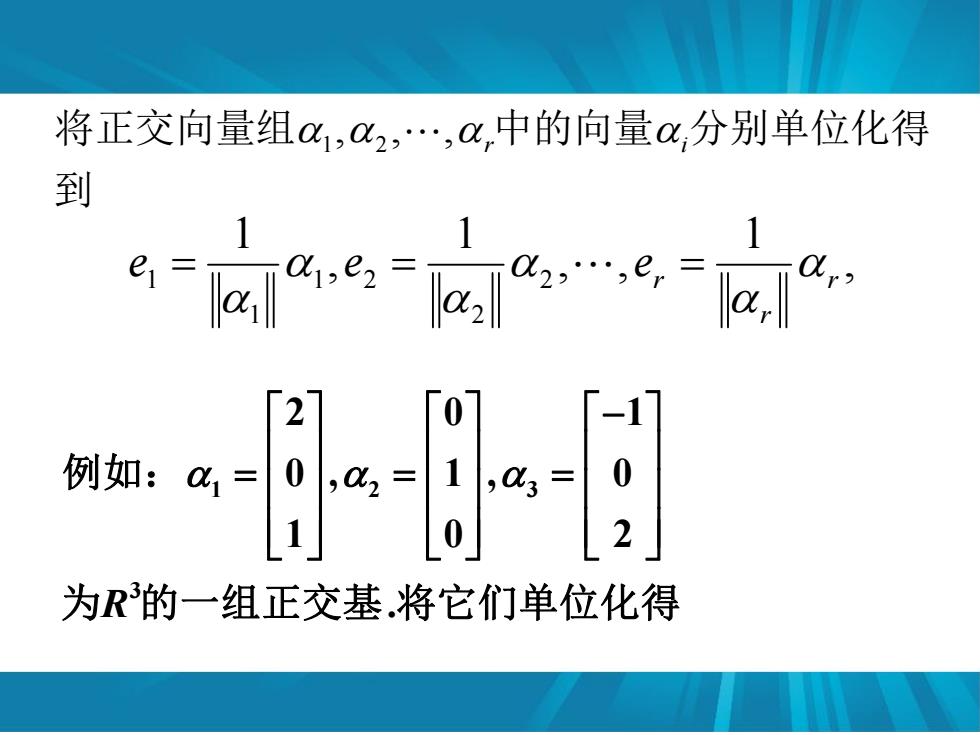
将正交向量组1,02,.,C,中的向量x,分别单位化得 到 2 0 -1 例如:a1=0,a2=1 ,C3= 0 1 2 为R的一组正交基.将它们单位化得
1 2 3 3 2 0 1 0 , 1 , 0 1 0 2 R . 例如: 为 的一组正交基 将它们单位化得 到 将正交向量组1 , 2 ,, r中的向量i分别单位化得 , 1 , , 1 , 1 2 2 1 2 1 1 r r r e e e