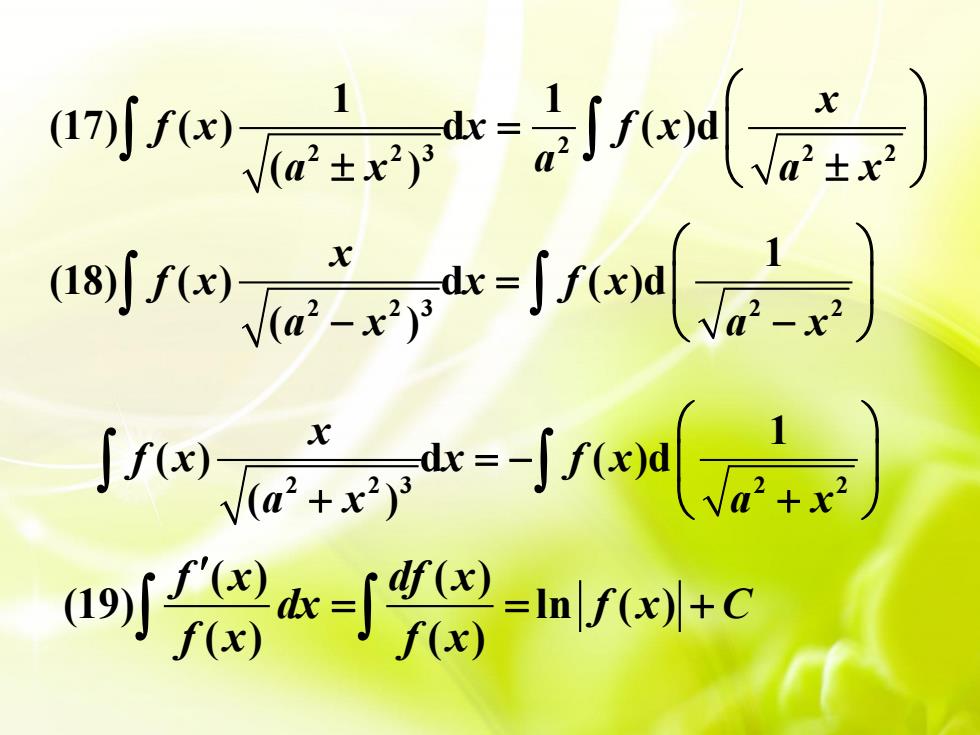
-xra(17)J f(x)dx =V(a ±x')3±x2Va?x(18)[ f(x)dx =J f(x)dx[ f(x)dx =-J f(x)dV(a’ +x")3Va?+x?f(x)df(x)(19)]=In|f(x)|+Cdx =f(x)f(x)
2 2 2 3 2 2 1 1 (17) ( ) d ( )d ( ) x f x x f x a x a x a = 2 2 3 2 2 1 (18) ( ) d ( )d ( ) x f x x f x a x a x = − − 2 2 3 2 2 1 ( ) d ( )d ( ) x f x x f x a x a x = − + + ( ) ( ) (19) ln ( ) ( ) ( ) f x df x dx f x C f x f x = = +

++dx.[(1--xdx.Dex(1+ 2lnx)rdx cos* x(1 + tanx)Intanxarctan x练习dxdxsin x cos x/x(1+x)
. (1 2ln ) 1 dx x x + 1 2 1 (1 ) . x x e dx x + − arctan ln tan (1 ) sin cos x x dx dx x x + x x 练习 2 d cos (1 tan ) x x x +

求例5ar22aX-1解dxdx222+xaa1+aX=+C.arctanaaaX1+a
例5 求 . 1 2 2dx a x + 解 dx a x + 2 2 1 dx a a x + = 2 2 2 1 1 1 + = a x d a a x 2 1 1 1 arctan . 1 C a x a = +

dx例6求(a>0)a?-x?dxdx1解:211-()ad(t)(一)ax=arcsin=+C(a>0)a作恒等变形是向着我们常用的积分公式努力
例6 求 2 2 ( 0) dx a a x − 解: − 2 2 a x dx − = 2 1 ( ) 1 a x dx a − = 2 1 ( ) ( ) a x a x d arcsin ( 0) x C a a = + 作恒等变形是向着我们常用的积分公式努力!

dx例7 求a?-x?dx解:dx2ar0aa+xXdxdx2aJ2adaa+x1-x1In|a-x|+CIn+X2a2a1a+x+CIn(a> 0)2aa-xdx1X一0类似地可推出+Cin(a>0)22aarx+a
例7 求 − 2 2 a x dx 解: − 2 2 a x dx dx a a x a x ) 1 1 ( 2 1 − = + − = + a x dx a x a dx a 2 1 2 1 1 1 ln | | ln | | 2 2 a x a x C a a = + − − + 1 ln | | ( 0) 2 a x C a a a x + = + − 类似地可推出 2 2 1 ln | | ( 0) 2 dx x a C a x a a x a − = + − +