
注:(1)定理说明:若已知f(u)du=F(u)+C则[ f[p(x)]g'(x)dx = F[p(x)]+ C即[ f(u)du= F(u)+C中的u换成了另一个变量x的可微函数(x)后,式子仍然成立又称为积分的形式不变性1(2)由定理可见,虽然 / f[p(x)]p'(x)dx是一个整体符号,但可把视为自变量微分—凑微分= Φ'(x)dx = dp(x)(3)凑微分法就在凑微分上,其基本思想就是对被积表达式进行变形,主要考虑如何变化(x)
注: (1) ( ) ( ) [ ( )] ( ) [ ( )] f u du F u C f x x dx F x C = + = + 定理说明:若已知 则 ( ) ( ) ( ) f u du F u C u x x = + 即 中的 换成了另一个 变量 的可微函数 后,式子仍然成立 ——又称为积分的形式不变性 (2) [ ( )] ( ) ( ) ( ) f x x dx dx x dx d x = 由定理可见,虽然 是一个整体符号,但可把 视为自变量微分 ——凑微分 (3)凑微分法就在凑微分上,其基本思想就是对 被积表达式进行变形,主要考虑如何变化f(x)
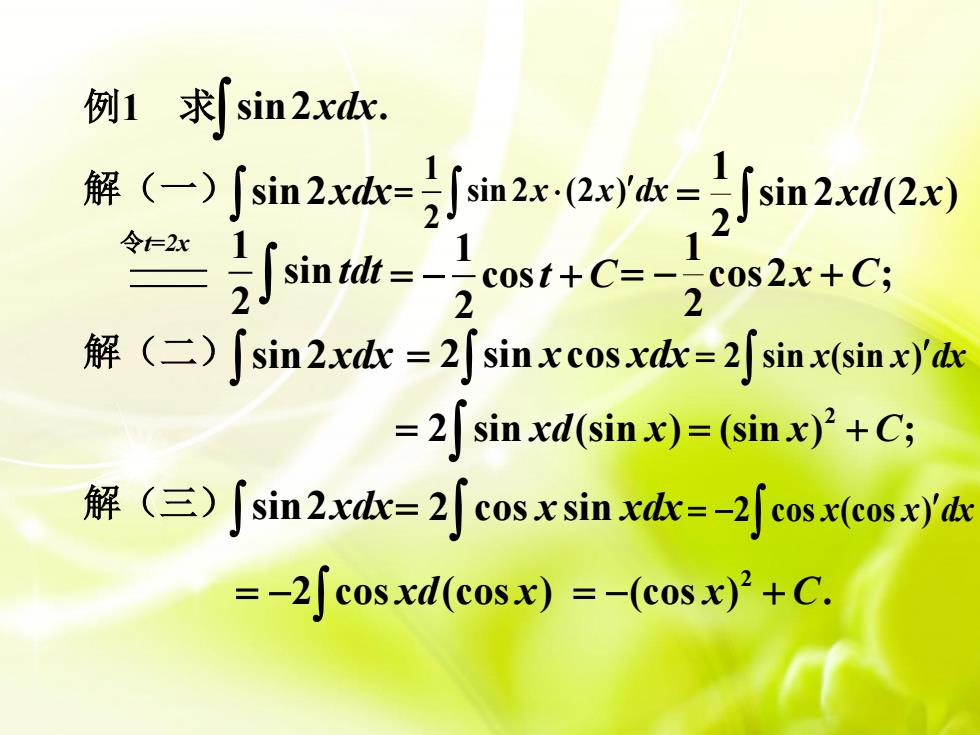
例1 求[ sin2xdx.11解(一)(sin2xdx=sin 2x· (2x)'dx :sin 2xd(2x)21令=2x-引1sin tdt = cos2x+C;二cost+C=-122解(二)[sin2xdx =2 sinxcosxdx=2[ sin x(sin x)'dx= 2J sin xd(sin x)=(sin x)° +C;解 (三) [ sin2xdx= 2[ cos x sin xdx=-2J cos x(cos x)'dx= -2f cos xd(cosx) = -(cos x) +C
例1 求 sin2 . xdx 解(一) sin2xdx = sin2 (2 ) 2 1 xd x cos2 ; 2 1 = − x + C 解(二) sin2xdx = 2 sin xcos xdx = 2 sin (sin ) xd x 2 = + (sin ) ; x C 解(三) sin2xdx= 2 cos sin x xdx = −2 cos xd(cos x) 2 = − + (cos ) . x C 1 sin 2 tdt 令t=2x 1 cos 2 = − +t C 1 sin 2 (2 ) 2 = x x dx = 2 sin (sin ) x x dx = −2 cos (cos ) x x dx

-求例2dx.3+2x111解(3 +2x),3+2x23+2x。dx=d(3+2x)3+2x2/3+2x-d=↓n/u/+C-↓m13+2x1+C.J f(ax+b)dx==] f(u)dulu=ax+b一般地adx = =d(ax + b)a
例2 求 . 3 2 1 dx x + 解 (3 2 ) , 3 2 1 2 1 3 2 1 + + = + x x x dx x 3 + 2 1 x dx x (3 2 ) 3 2 1 2 1 + + = du u = 1 2 1 = ln | u | +C 2 1 ln | 3 2 | . 2 1 = + x +C f (ax + b)dx = u=ax+b f u du a [ ( ) ] 1 一般地 1 d d( ) x ax + b a = d(3 2 ) + x

例3.求I (ax + b)" dx.解: 当m±-1时令u=ax+b,则du=adx,故1 1原式=[um-du_-m+1+Cuam+1a1(ax + b)m+1 + Ca(m+1)当m =-1时dx- In|ax+b|+Cax+b1
( ) d . m a x b x + 解: 令u a x b = + , 则 d d , u a x = 故 原式 = 1 d m u u a 1 1 1 1 m u C a m + = + + 1 1 ( ) ( 1) m ax b C a m + = + + + 当m = −1时 d 1 ln x a x b C a x b a = + + + 当m −1时 例3. 求

例4drS(2 + x)解令2+x=u则x=u-2 dx =du2(u-2)2dx=du(2 + x)3s-J(ul -4u? + 4u-du2C= ln十U人24+C= Inx+2|+(x + 2)?x+2
例 4 2 3d (2 ) x x + x 解 令2 = + x u 则x u= 2 −2 3 ( 2) d u u u− = 2 4 2 ln 2 2 ( 2) x C x x = + + − + + + d d x u = 2 3d (2 ) x x + x ( ) 1 2 3 u u u u 4 4 d − − − = − + 2 4 2 ln u C u u = + − +