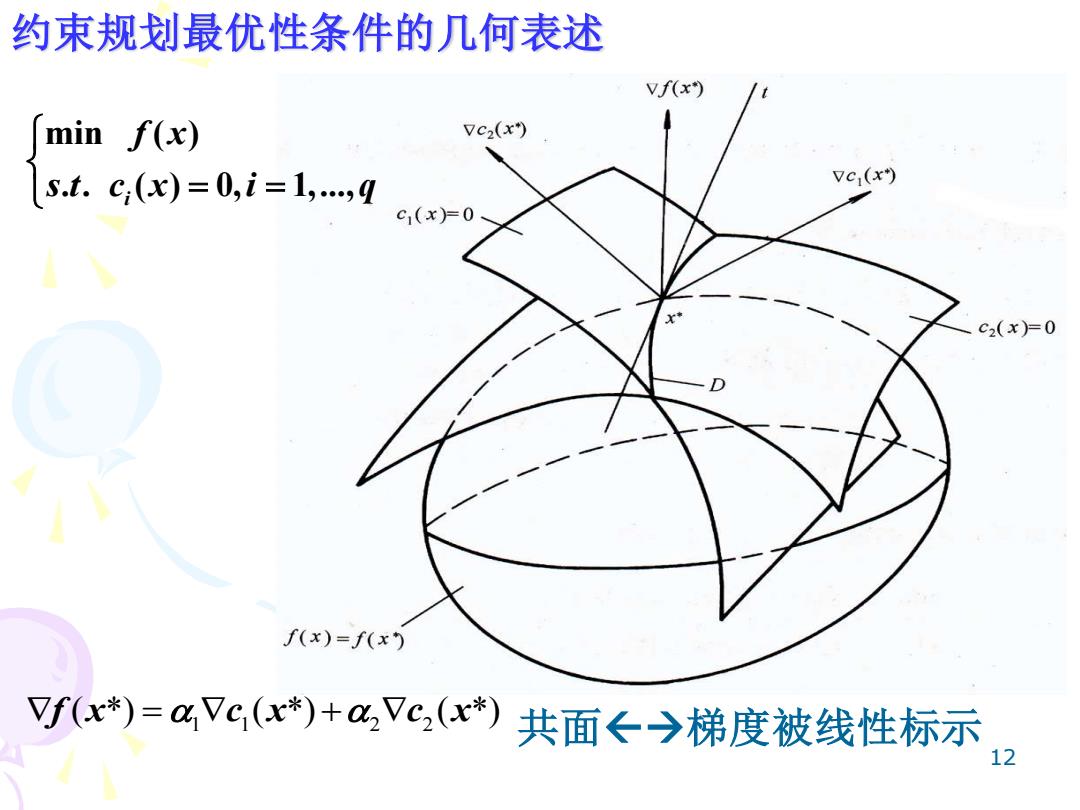
约束规划最优性条件的几何表述 vf(x) min f(x) Vc2(x) 5.t.c(x)=0,i=1,…,9 Vc (x) e(x)-0 c2(x)=0 f(x)=f(x) Vf(x*)=aVc,(x*)+,Vc,(x)共面←→梯度被线性标示
12 共面→梯度被线性标示 约束规划最优性条件的几何表述 1 1 2 2 = + f x c x c x ( *) ( *) ( *) min ( ) . . ( ) 0, 1,..., i f x s t c x i q = =
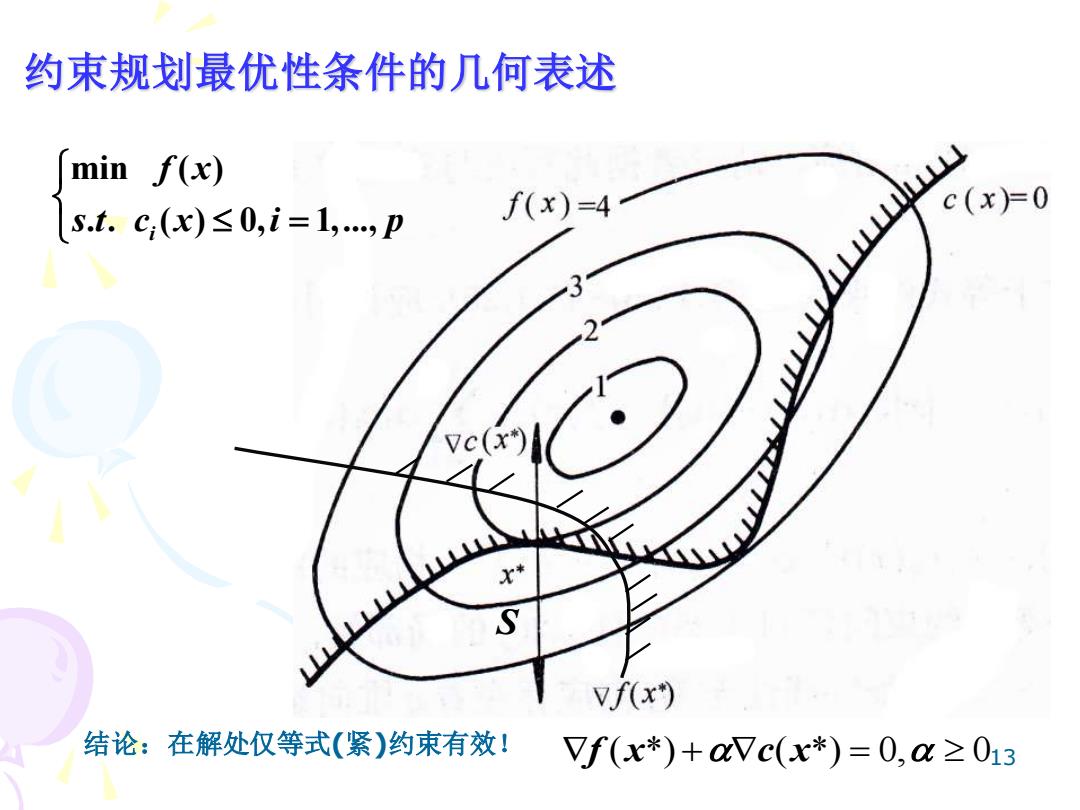
约束规划最优性条件的几何表述 min f(x) S.t.c(x)≤0,i=1,,p f(x)=4 c(x=0 7c(x) vf(x) 结论:在解处仅等式(紧)约束有效! Vf(x*)+avc(x*)=0,a=013
13 min ( ) . . ( ) 0, 1,..., i f x s t c x i p = 结论:在解处仅等式(紧)约束有效! 约束规划最优性条件的几何表述 + = f x c x ( *) ( *) 0, 0 S
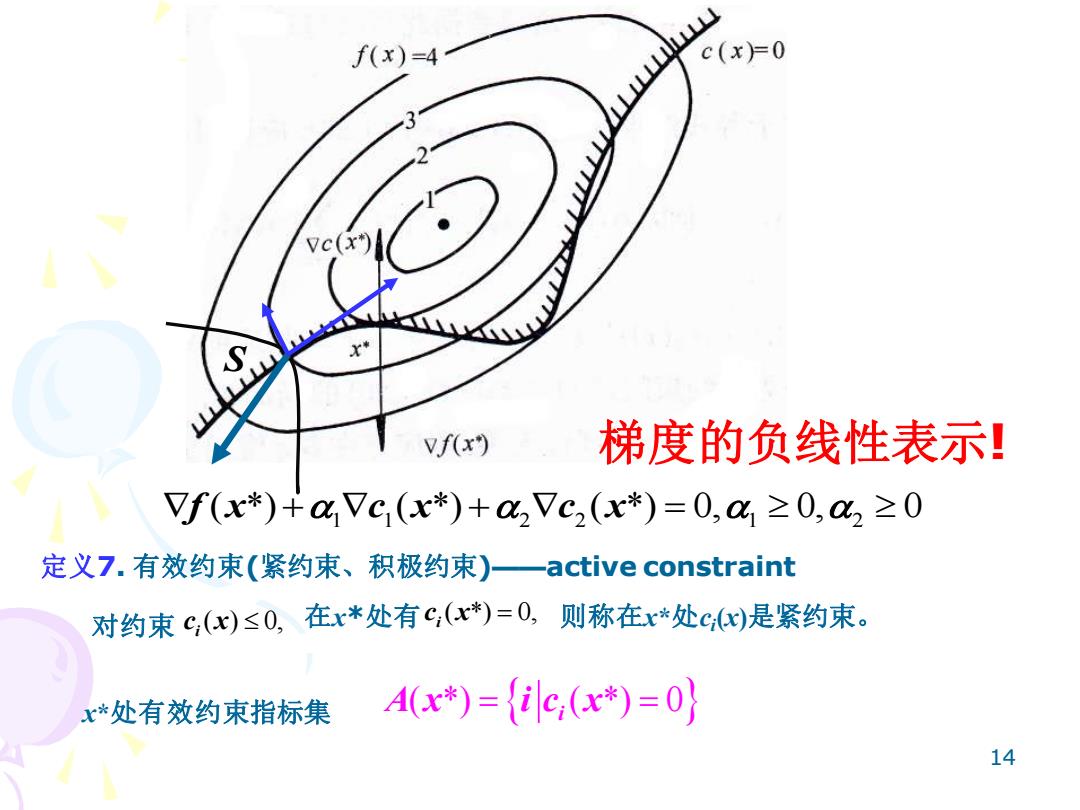
f(x)=4 c(x=0 Vc(x的 vf(x) 梯度的负线性表示! Vf(x*)+aVc(x*)+a2Vc2(x*)=0,c1≥0,a2≥0 定义7.有效约束(紧约束、积极约束)一active constraint 对约束C,(x)≤0, 在x*处有C,(x*)=0,则称在x*处c)是紧约束。 x*处有效约束指标集 A(x*)={ilc,(x*)=0} 14
14 对约束 定义7. 有效约束(紧约束、积极约束)——active constraint c x i ( ) 0, 在x*处有 c x i ( *) 0, = 则称在x*处ci (x)是紧约束。 x*处有效约束指标集 A x i c x ( *) ( *) 0 = = i 梯度的负线性表示! 1 1 2 2 1 2 + + = f x c x c x ( *) ( *) ( *) 0, 0, 0 S

约束规划最优性必要条件 定理:(约束问题解的必要条件)对一般可微规划问题 min f(x) s.t.c,(x)≤0,i=1,,p c,(x)=0,i=p+1,,p+q 设x*是问题的局部解,若x*处的有效约束的梯度向量Vc,(x*)i∈A(x*) 线性无关,或者所有约束函数是线性函数,则存在p叶q维向量 *=(a,a,…,apg使得 f*+2a,vc,()=0 Karush-Kuhn-Tucker i= 条件—KKT条件 C(x*)≤0,a*≥0,0x,*c,(x*)=0,i=1,2,…2D cce)-Bi-plp 令g(e)=(G(x,C,(x》,(x)=(Cp4(x,,cpHn() 量化表示 互补 松弛 条件 min f(x) Vf(x*)+vg(x*)u*+h(x*)v*= s.t. g6x≤0 gx*)≤0,*≥0,w*rg(x*)=0 h(x)=0 h(x*)=0,y∈R 15
15 定理:(约束问题解的必要条件)对一般可微规划问题 min ( ) . . ( ) 0, 1,..., ( ) 0, 1,..., i i f x s t c x i p c x i p p q = = = + + 设 x* 是问题的局部解,若 x* 处的有效约束的梯度向量 ( *)( ( *)) i c x i A x 线性无关,或者所有约束函数是线性函数,则存在 p+q 维向量 ( ) * * * 1 2 * , , , = + T p q 使得 1 1 ( ) ( ( ),..., ( )) , ( ) ( ( ),..., ( )) T T p p p p g x c x c x h x c x c x 令 = = + + min ( ) . . 0 ( ) 0 f x s t g(x) h x = 向量化表示 约束规划最优性必要条件 1 ( *) * ( *) 0 ( *) 0, * 0, * ( *) 0, 1,2, , ( *) 0, 1,2, , p q i i i i i i i i f x c x c x c x i p c x i p p q + = + = = = = = + + ( *) ( *) * ( *) * 0 ( *) 0, * 0, * ( *) 0 ( *) 0, + + = = = T q f x g x u h x v g x u u g x h x v R Karush-Kuhn-Tucker 条件——KKT条件 互补 松弛 条件

Lagrange函数 Lx,)fx)+∑a,c(x) (a,≥0,i=1,2,…,p) i=1 L(x,u,v)=f(x)+u'g(x)+v"h(x) (u≥0) Lagrange乘子:o,或w,y 互补松弛条件:C,(x*)≤0,C*≥0,a,*c,(x*)=0,i=1,2,…,p or g(x*)≤0,*≥0,u*gx*)=0VL(x,u,y)=0 Karush-Kuhn-Tucker条件—KKT条件 u≥0,ug(x)=0 约束规格 约束限制(规范)条件 h(x)=0 1)有效约束的梯度向量Vc,(x*i∈A(x)线性无关; 2) 所有约束都是线性函数; 3) 16
16 Lagrange函数 ( *) , * , * ( *) , , , , 0 0 0 1 2 i i i i c x c x i p = = ( , , ) 0 0, ( ) 0 ( ) 0 x T L x u v u u g x h x = = = Karush-Kuhn-Tucker条件——KKT条件 1 ( , )= ( ) ( ) ( 0, 1,2, , ) ( , , ) ( ) ( ) ( ) ( 0) p q i i i i T T L x f x c x i p L x u v f x u g x v h x u + = + = = + + Lagrange乘子: i 或u v , 互补松弛条件: ( *) 0, * 0, * ( *) 0 = T or g x u u g x 约束规格——约束限制(规范)条件 1) 有效约束的梯度向量 ( *)( ( *)) i c x i A x 线性无关; 2) 所有约束都是线性函数; 3) ……