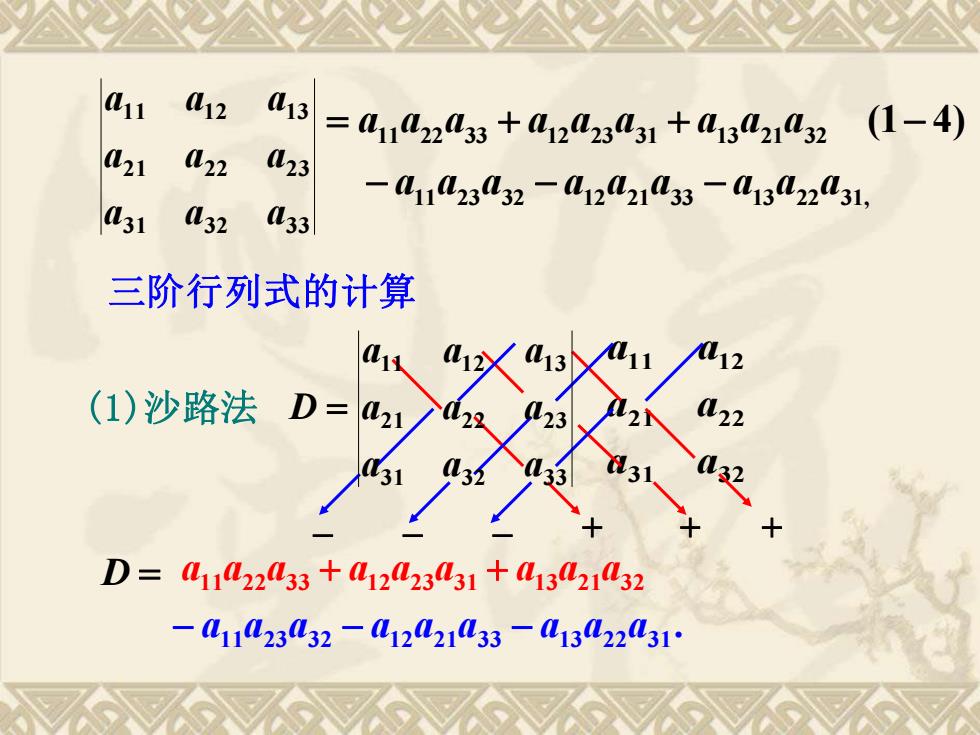
11 12 3 =41142233+41223431+41321L32(1-4) L21 L22 23 -41102332-0120213-01302L31, L31 l32 33 三阶行列式的计算 12 L13 (1)沙路法D= D=41122433+012023431+132132 -41123L32-01221L33一L13L2231
31 32 21 22 11 12 a a a a a a − − − + + + . − a11a23a32 − a12a21a33 − a13a22a31 (1)沙路法 三阶行列式的计算 D = a11a22a33 + a12a23a31 + a13a21a32 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = 11 22 33 12 23 31 13 21 32 11 23 32 12 21 33 13 22 31, a a a a a a a a a (1 4) a a a a a a a a a = + + − −−− 31 32 33 21 22 23 11 12 13 a a a a a a a a a

(2)对角线法则 =411422033+012023031+13021L32 -41342231-122133-11L23032 注意 红线上三元素的乘积冠以正号,蓝线上三 元素的乘积冠以负号. 说明1.对角线法则只适用于二阶与三阶行列式
31 32 33 21 22 23 11 12 13 a a a a a a a a a = a11a22a33 . 11 23 32 − a a a (2)对角线法则 注意 红线上三元素的乘积冠以正号,蓝线上三 元素的乘积冠以负号. 说明1. 对角线法则只适用于二阶与三阶行列式. + a12a23a31 + a13a21a32 13 22 31 − a a a 12 21 33 − a a a

2.三阶行列式包括3!项,每一项都是位于不同行 不同列的三个元素的乘积,其中三项为正,三项为 负. 利用三阶行列式求解三元线性方程组 011X1+412X2+413X3=b1, 如果三元线性方程组 {021k1+22x2+23x3=b2, 431X1+32X2+33X3=b3; 11 L12 3 的系数行列式D= L21 L22 L23 ≠0, 031 L32 33
如果三元线性方程组 + + = + + = + + = ; , , 3 1 1 3 2 2 3 3 3 3 2 1 1 2 2 2 2 3 3 2 1 1 1 1 2 2 1 3 3 1 a x a x a x b a x a x a x b a x a x a x b 的系数行列式 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = 0, 利用三阶行列式求解三元线性方程组 2. 三阶行列式包括3!项,每一项都是位于不同行, 不同列的三个元素的乘积,其中三项为正,三项为 负

11 12 13 b 记 12 3 D= 021 L22 L23 D1=b2 L22 L237 a31 L32 33 b3 32 33 11 b 13 11 12 b D2=M21 b2 237 D3=21 022 b 431 b3 33 31 32 ba 则三元线性方程组的解为: X3= D
, 31 3 33 21 2 23 11 1 13 2 a b a a b a a b a D = . 31 32 3 21 22 2 11 12 1 3 a a b a a b a a b D = 则三元线性方程组的解为: , 1 1 D D x = , 2 2 D D x = . 3 3 D D x = 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = , 3 32 33 2 22 23 1 12 13 1 b a a b a a b a a D = 记