西安电子科技大学：《概率论与数理统计》课程教学课件（讲稿）第八章 假设检验 8.3 正态总体方差的假设检验 8.6 分布拟合检验

§8.3正态总体方差的假设检验 小结 本节学习的正态总体均值的假设检验有： 1.单个总体均值的检验一一U检验；t检验 2.单个正态总体方差的梅验法一一Y2检验法； 3.两个总体均值羞，-μ，的检验一一U检验，t检验， 4.两个正态总体方差的验法一一F检验法； 5.基于成对数据的检验一一t检验： 正态总体均值、方差的检验法见下表 (显著性水平为a) 16/57

小结 本节学习的正态总体均值的假设检验有: 1.单个总体均值的检验 — — U检 验; t检 验 3. U t ; 两个总体均值差1  2 的检验 — — 检验，检 验 5. 基于成对数据的检验— — t 检 验; 正态总体均值、方差的检验法见下表 ( 显著性水平为 ) . ; 2 单个正态总体方差的检验 法 — —  2 检验法 4. 两个正态总体方差的检验 法 — — F 检验法; §8.3 正态总体方差的假设检验 16/57

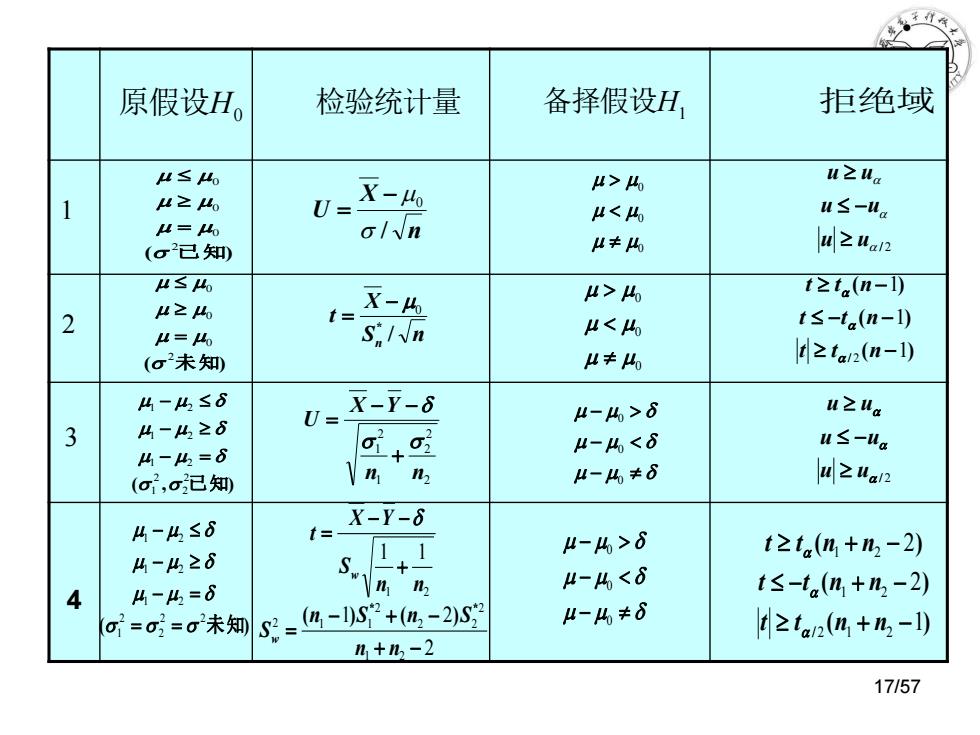
原假设H。 检验统计量 备择假设H, 拒绝域 H≤Ao -40 I>46 u之ua u≥46 Us: L<4 u≤-ua 4=46 GIn (σ已知) L≠% u≥ua12 A≤ X-4 4>46 t≥ta(n-l) 2 4≥4 S,In μ<4 t≤-ta(n-l) A=6 (σ未知 4≠6 d≥ta2(n-l) 4-4≤6 4-4≥6 V= X-Y-δ 4-4>6 u≥ua 3 μ-A<8 l≤-ua %-42=6 (σ，o已知 mn H-%≠6 4≥ua2 4-4≤6 x-Y-6 4-4>6 4-4≥6 t≥ta(m+m2-2) 4-4=6 u-4<6 4 t≤-ta(n+n-2) σ=o1=σ2未知 82=4-19+,-2S 4-4≠6 t≥ta2(m+n-1） n+2-2 17157

4 ( 未知) 2 2 2 21 1 2 1 2 1 2                                   000 ( ) ( ) ( ) / 122 2 1 2 1 2 1 2           t t n n t t n n t t n n   2 1 2 1 1 1 2 2 2 2 2 2 1 1 1 2           n n n S n S S n n SX Y t w w * * ( ) ( )  原假设H0 检验统计量 备择假设H1 拒绝域 ( 已知) 2 000       ( 未知) 2 000       ( , 已知) 22 211 2 1 2 1 2                  n X U  / 0  S n X t n / *  0  222 121 n n X Y U      000       000                     000  / 2  u u u u u u   ( ) ( ) ( ) / 111  2       t t n t t n t t n    / 2  u u u u u u   321 17/57

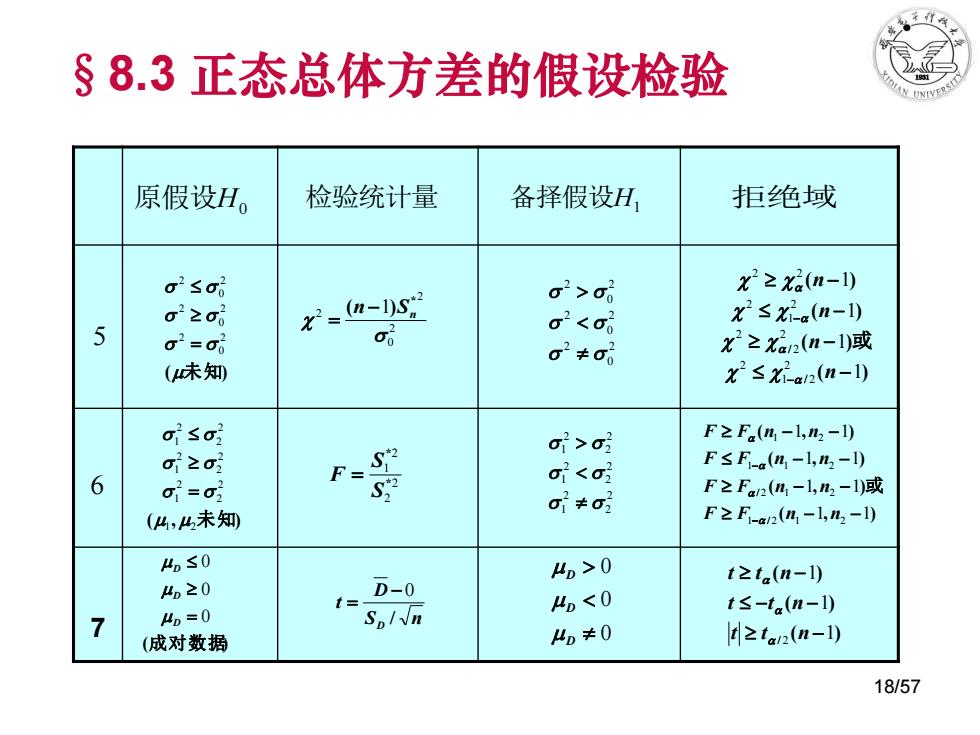
§8.3正态总体方差的假设检验 原假设H。 检验统计量 备择假设H, 拒绝域 o2≤o x2≥x2n-l) Gi2ag x2=n-10S2 02> x2≤x2a(n-) 5 σ2<o g2=00 02+06 x2≥Xa2(n-1)或 (未知 X2≤Xa2(n-l) aisa Gi>G2 F≥Fa(n1-1,n2-l) σ22o 6 gi=02 F s ai<a F≤F-a(n-l,n2-l) F之F2(n-l,m2-1)减 o≠o (4,4未知 F≥F-a2(m1-l,n2-l) 4D≤0 4o>0 4D20 t=D-0 t≥ta(n-) 4=0 SpIn ,≤0 t≤-ta(n-l) (成对数据 4D≠0 |t≥ta2(n-l) 18/57

7 原假设H0 检验统计量 备择假设H1 拒绝域 ( , 未知) 1 2 2 2 2 1 2 2 2 1 2 2 2 1            (成对数据) 0 0 0    D D D    S n D t D /  0  0 0 0    D D D    ( ) ( ) ( ) / 1 1 1  2       t t n t t n t t n    (未知)       2 0 2 2 0 2 2 0 2    2 0 2 2 1   * ( ) n  Sn  2 2 2 1 * * S S F  2 0 2 2 0 2 2 0 2          2 2 2 1 2 2 2 1 2 2 2 1          ( ) ( ) ( ) ( ) / / 1 1 1 1 2 1 2 2 2 2 2 2 1 2 2 2           n n n n             或 ( , ) ( , ) ( , ) ( , ) / / 1 1 1 1 1 1 1 1 1 2 1 2 2 1 2 1 1 2 1 2               F F n n F F n n F F n n F F n n     6 或 5 §8.3 正态总体方差的假设检验 18/57

§8.3正态总体方差的假设检验 原假设H。 检验统计量 备择假设H 拒绝域 μ≤4 μ>4 z22a 1 I≥4 z治 B<o z≤-2a I=46 (o已知) μ≠ ≥zan 4≤46 4>46 t≥a(n-l) 2 H≥46 t≤-.(n-l) I=46 (σ2未知) 2tan(n-1) 4-h2≤6 t≤-ta(n1+n2-2) 222a 3 4-4226 :≤-a 4-=6 (o,o记知) ≥a2 4-4≤8 X-7-6 I=- I-4>6 1≥1.(m+n2-2) 4-42≥6 I-4<δ 1≤-4(n+n3-2) 4 4-42=6 (o=o=σ2未知) S:=a-0S+m,-2S I-46≠6 21a2n+n2-l) %+n2-2 19/57

4 原假设H0 检验统计量 备择假设H1 拒绝域 ( ) 2 0 0 0  已知          ( ) 2 0 0 0  未知          ( , ) 2 2 2 1 1 2 1 2 1 2   已知                n X Z / 0     S n X t /  0  2 2 2 1 2 1 n n X Y Z        0 0 0          0 0 0                         0 0 0  / 2   z z z z z z     ( 1) ( 1) ( 1)  / 2       t t n t t n t t n     / 2   z z z z z z     ( ) 2 2 2 2 1 1 2 1 2 1 2    未知                                 0 0 0 ( 1) ( 2) ( 2) / 2 1 2 1 2 1 2           t t n n t t n n t t n n    2 ( 1) ( 2) 1 1 1 2 2 2 2 2 2 1 1 1 2           n n n S n S S n n S X Y t w w  ( 2) t  t n1  n2  3 2 1 §8.3 正态总体方差的假设检验 19/57