
第四章线性方程组 线性方程组与几何联系 从几何角度考虑线性方程组 411x1+412x2=b1 021X1+42X2=b2 每一个方程均对应于平面上的一条直线 求解方程组,相当于求两条直线的交点:
第四章 线性方程组 线性方程组与几何联系 从几何角度考虑线性方程组 每⼀个方程均对应于平面上的⼀条直线. 求解方程组, 相当于求两条直线的交点. 11 1 12 2 1 21 1 22 2 2 a x a x b a x a x b + = + =
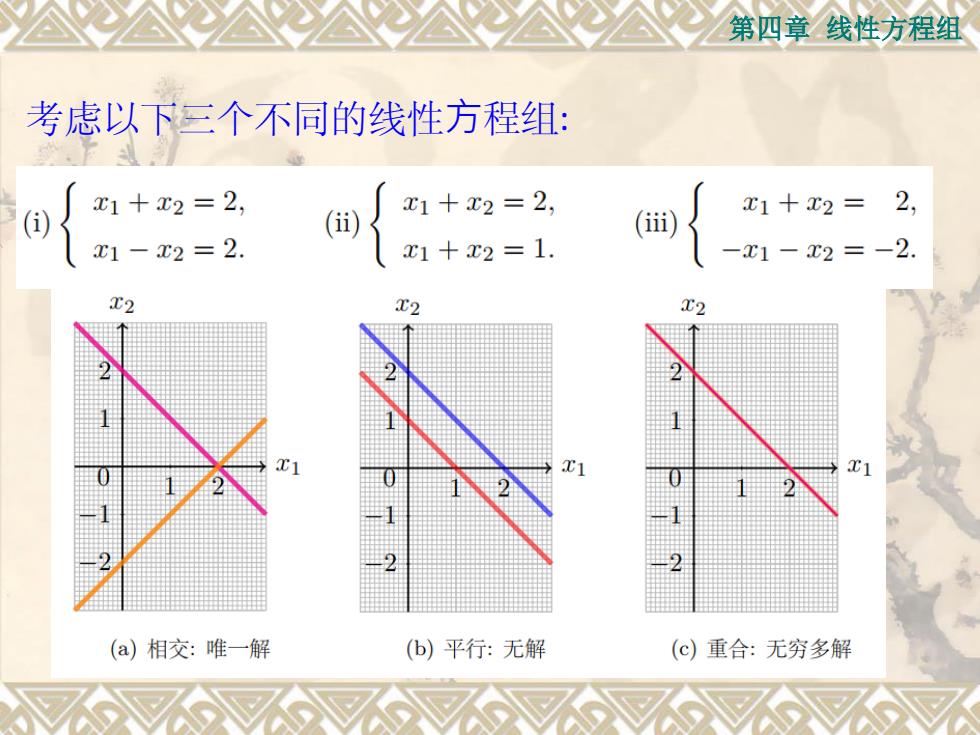
第四章线性方程组 考虑以下三个不同的线性方程组: x1+x2=2, x1+x2=2, x1+x2=2, ) () () C1-x2=2. x1+x2=1. -x1-x2=-2. T2 T2 (a)相交:唯一解 (b)平行:无解 (c)重合:无穷多解
第四章 线性方程组 考虑以下三个不同的线性⽅程组:

第四章线性方程组 两条直线之间的关系有三种情况:相交、平行、重合. 相应地,一个线性方程组的解,有下列三种情况: (1)唯一解 (2)无解 (3)无穷多解
第四章 线性方程组 两条直线之间的关系有三种情况: 相交、平行、重合. 相应地,⼀个线性方程组的解, 有下列三种情况: (1)唯一解 (2)无解 (3)无穷多解

第四章线性方程组 二、线性方程组解的判别 1 + X2 2x3 1, 2X1 一 X2 + 2x3 4, 例1:解线性方程组 X1 2X2 3, 4x 十 4x3 2
第四章 线性方程组 例1:解线性方程组 1 2 3 1 2 3 1 2 1 2 3 2 1, 2 2 4, 2 3, 4 4 2. x x x x x x x x x x x ++= − + = − = ++= 二、线性方程组解的判别

第四章线性方程组 解: 1 2 2 2 -1 2 4 0 -3 -2 2 (A,b)= 1 -2 0 3 3 -2 2 4 4 2 0 -3 -4 -2 1 1 2 1 2 0 -3 -2 2 0 1 2/3 -2/3 0 0 0 0 0 0 1 2 0 0 2 A 0 0¥0 0
第四章 线性方程组 解: 1 1 2 1 2 1 2 4 ( , ) 1 2 0 3 4 1 4 2 A b − = − 1 1 2 1 0 3 2 2 ~ 0 3 2 2 0342 − − − − −−− 1 1 2 1 0 3 2 2 ~ 0 0 0 0 0 0 2 4 − − − − 1 1 2 1 0 1 2/ 3 2/ 3 ~ 0 0 1 2 0 0 0 0 −