用入表示所有小弧段的最大长度,如果当入→>0时, 的极限总存在,则称其为P(xy)在有 向曲线弧L上对坐标x的曲线积分,记为: 同理当入-→0时, (5,n 的极限总存在,则称其为Qx,y) 在有向曲线弧L上对坐标y的曲线 积分,记为: HIGH EDUCATION PRESS
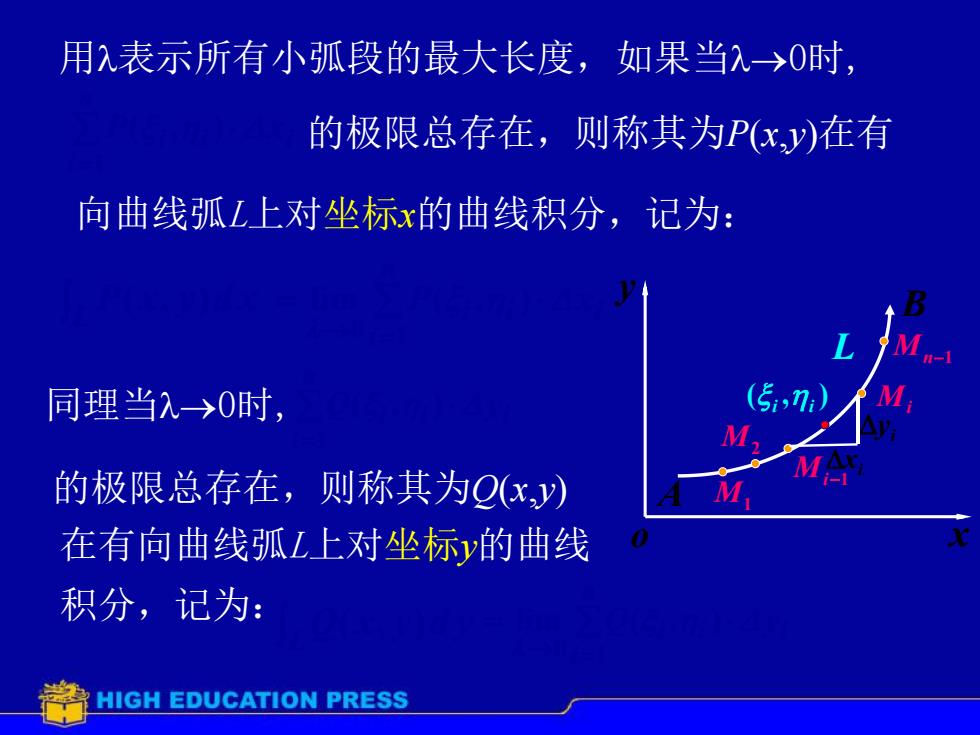
o x y A B Mn1 Mi Mi1 M2 M1 ( , ) i i L xi i y 用表示所有小弧段的最大长度,如果当0时, i n i i i P x 1 ( , ) 的极限总存在,则称其为P(x,y)在有 向曲线弧L上对坐标x的曲线积分,记为: L P(x, y)d x i n i P i i x 1 0 lim ( , ) 同理当0时, i n i i i Q y 1 ( , ) 的极限总存在,则称其为Q(x,y) 在有向曲线弧L上对坐标y的曲线 积分,记为:LQ( x, y)d y i n i i i Q y 1 0 lim ( , )

被积函数 ,Q(,)= lim ∑2(5,7)·4 积分和式 积分弧段 坐标微分 对坐标的曲线积分统称为第二类曲线积分 平面变力F(x,)=P(x,yi+(,)i 沿L所作的功 若记 则 HIGH EDUCATION PRESS
L P( x, y)d x i n i P i i x 1 0 lim ( , ) 对坐标的曲线积分统称为第二类曲线积分 被积函数 积分弧段 积分和式 LQ(x, y)dy lim ( , ) . 1 0 n i i i i Q y 坐标微分 F x y P x y i Q x y j 平面变力 ( , ) ( , ) ( , ) 沿L所作的功 L L W P(x, y)d x Q(x, y)d y L P(x, y)d x Q(x, y)d y 简记为 若记 dr dx i dy j, 则 L W F x y dr ( , )

几点说明: (1)所谓“对坐标的曲线积分”,有两个特征: ·积分和是在有向曲线弧L上作出的; ·积分和中的微元素是有向小弧段所对应的关于 坐标x和y的增量。 即被积表达式中的微分是关于坐标x和y的微分。 (2)当P(x,),Q(x,y)在有向光滑曲线弧L上连续, 第二类曲线积分都存在。 (3)L可以推广到分段光滑的情形:L=L1+2 HIGH EDUCATION PRESS
(1)所谓“对坐标的曲线积分” ,有两个特征: • 积分和是在有向曲线弧L上作出的; • 积分和中的微元素是有向小弧段所对应的关于 坐标x和y 的增量。 几点说明: 即被积表达式中的微分是关于坐标x和y的微分。 (2)当P (x , y) , Q (x , y)在有向光滑曲线弧L上连续, 第二类曲线积分都存在。 (3)L 可以推广到分段光滑的情形:L L1 L2 LF x y dr ( , ) 1 ( , ) L F x y dr L P( x, y)d x i n i P i i x 1 0 lim ( , ) 2 ( , ) L F x y dr

(4)推广至空间的情形 P(,y,)在空间有向曲线弧下上对坐标x的曲线积分为 同理 若记 则 HIGH EDUCATION PRESS
P(x, y,z)在空间有向曲线弧 上对坐标x的曲线积分为 P(x, y,z)dx (4)推广至空间的情形 同理 Q(x, y,z)dy lim ( , , ) . 1 0 i n i P i i i x lim ( , , ) . 1 0 i n i i i i Q y R( x, y,z)dz i n i i i i R z 1 0 lim ( , , ) Pd x Qd y Rd z Pdx Qdy Rd z 简记为 若记 A(x, y,z) P(x, y,z)i Q(x, y,z) j R(x, y,z)k, 则 dr dx i dy j dz k, Pdx Qdy Rd z A x y z dr ( , , )

3.性质 P(x,y)dx+(x,y)dy=F(x,y)dr ∫IaF)士BF(x小d =a,F(x,y在+p,F(x,y山 (2)若L可分成k条有向光滑曲线弧上,(1=1·,k) 则 P(x.y)dx+O(x.y)dy 注:第一类曲线积分中的不等式保号性质在此不成立 HIGH EDUCATION PRESS
3. 性质 (2) 若 L 可分成 k 条有向光滑曲线弧 L ( i 1, , k), i L P(x, y)dx Q(x, y)dy k i Li P x y x Q x y y 1 ( , )d ( , )d 则 机动 目录 上页 下页 返回 结束 1 2 (1) [ ( , ) ( , )] L F x y F x y dr L L P x y dx Q x y dy F x y dr ( , ) ( , ) ( , ) L L F x y dr F x y dr ( , ) ( , ) 1 2 注:第一类曲线积分中的不等式保号性质在此不成立