
导期 2.填空: 一 般地,设函数y=fx)的定义域为D,且ICD: (1)如果对任意x1水2∈I,当x1<x2时,都有 ,则称y=fx) 在I上是增函数(也称在I上单调递增); (2)如果对任意x1水2∈I,当x1<x2时,都有 ,则称y=x) 在I上是减函数(也称在I上单调递减), 两种情况下,都称函数在I上具有 (当为区间时,称为函 数的单调区间,也可分别称为单调递增区间或单调递减区间)
导航 2.填空: 一般地,设函数y=f(x)的定义域为D,且I⊆D: (1)如果对任意x1 ,x2∈I,当x1<x2时,都有f(x1 )<f(x2 ) ,则称y=f(x) 在I上是增函数(也称在I上单调递增); (2)如果对任意x1 ,x2∈I,当x1<x2时,都有f(x1 )>f(x2 ) ,则称y=f(x) 在I上是减函数(也称在I上单调递减). 两种情况下,都称函数在I上具有单调性(当I为区间时,称I为函 数的单调区间,也可分别称为单调递增区间或单调递减区间)
3.做一做:(1)若函数y=fx)在区间1,+∞)内是减函数,则f3)和 ⑤)的大小关系是 (2)已知函数y=fx),x∈[-4,7]的图象如图所示,则函数fx)的单 调递增区间是 (3)若函数fx)在区间(-5,-1)内是减函数,在区间(1,5)内是增函 数,则fx)可以是 (写出一个即可)
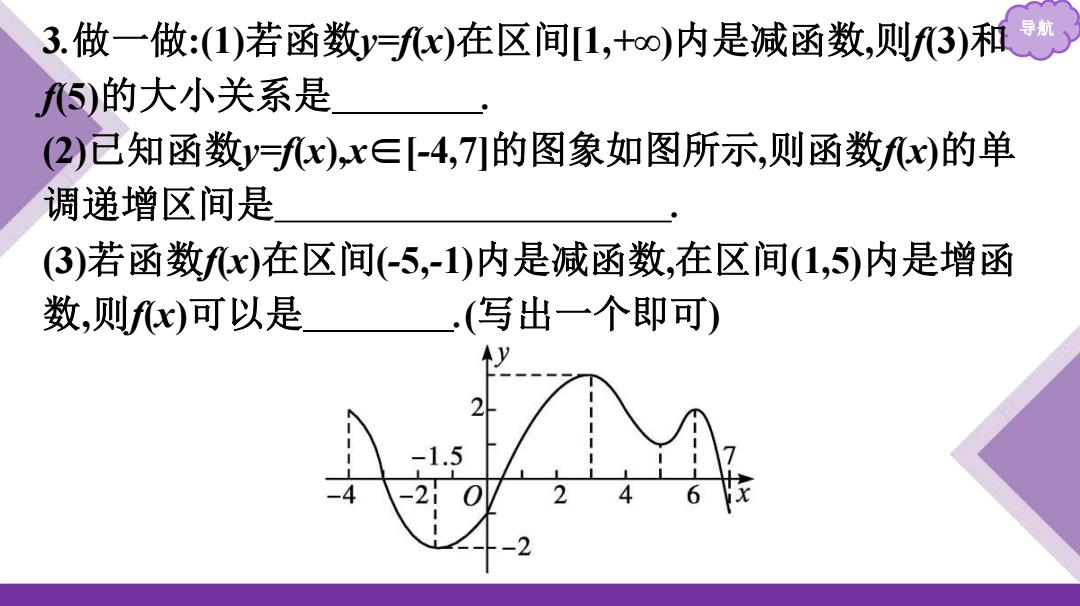
导航 3.做一做:(1)若函数y=f(x)在区间[1,+∞)内是减函数,则f(3)和 f(5)的大小关系是 . (2)已知函数y=f(x),x∈[-4,7]的图象如图所示,则函数f(x)的单 调递增区间是 . (3)若函数f(x)在区间(-5,-1)内是减函数,在区间(1,5)内是增函 数,则f(x)可以是 .(写出一个即可)

导航 解析:(1)因为函数y=x)在区间[1,十o)内是减函数,3<5, 所以f3)>5) (2)由图象知,fx)的单调递增区间为[-1.5,3]和[5,6. 答案:(13)>5) (2)[-1.5,3]和[5,6] (3)x)=x2(答案不唯一)
导航 解析:(1)因为函数y=f(x)在区间[1,+∞)内是减函数,3<5, 所以f(3)>f(5). (2)由图象知,f(x)的单调递增区间为[-1.5,3]和[5,6]. 答案:(1)f(3)>f(5) (2)[-1.5,3]和[5,6] (3)f(x)=x2 (答案不唯一)

【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“V,错误 的画“X” (1)如果函数fx)在区间(a,b)和(c,)内都是减函数,则fx)在区 间(a,b)U(c,)内是减函数.(X) (2)用定义证明函数的单调性时,可设x2,也可设x1>x2(√) 3)证明函数的单调性时,在该区间内取几个值验证一下即可 (X)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)如果函数f(x)在区间(a,b)和(c,d)内都是减函数,则f(x)在区 间(a,b)∪(c,d)内是减函数.( ) (2)用定义证明函数的单调性时,可设x1<x2 ,也可设x1>x2 . ( ) (3)证明函数的单调性时,在该区间内取几个值验证一下即可. ( ) × √ ×

导 课堂·重难突破 探究一由函数的图象确定函数的单调性或单调区间 【例1】作出函数fx)=x2+2x-31的图象,并指出其单调区间, 解:令g(x)=x2+2x-3=(x+1)2-4 先作出g()的图象,保留其在x轴及x轴上方部分, -2 把它在x轴下方的图象翻到轴上 -10123x 方就得到fx)=x2+2x-3的图象,如图所示. 由图象易得,函数fx)的单调递增区间是[-3,-1],1,+oo);函数c 的单调递减区间是(-o0,-3],1,1
导航 课堂·重难突破 探究一由函数的图象确定函数的单调性或单调区间 【例1】作出函数f(x)=|x2+2x-3|的图象,并指出其单调区间. 解:令g(x)=x2+2x-3=(x+1)2 -4. 先作出g(x)的图象,保留其在x轴及x轴上方部分, 把它在x轴下方的图象翻到x轴上 方就得到f(x)=|x2+2x-3|的图象,如图所示. 由图象易得,函数f(x)的单调递增区间是[-3,-1],[1,+∞);函数f(x) 的单调递减区间是(-∞,-3],[-1,1]