《线性代数》课程教学课件（PPT讲稿，C）第四章 线性方程组 4-1 线性方程组的解的判别

第四章线性方程组 二、线性方程组解的判别 定理4.1.1线性方程组(4-1)有解的充分必要条件是 它的系数矩阵4与增广矩阵有相同的秩，即R()=R(). 证对于一般线性方程组(4-1)，设 w 2 b W 2 01= ,02= ,“,0n= ,B= m2」 mn」 b

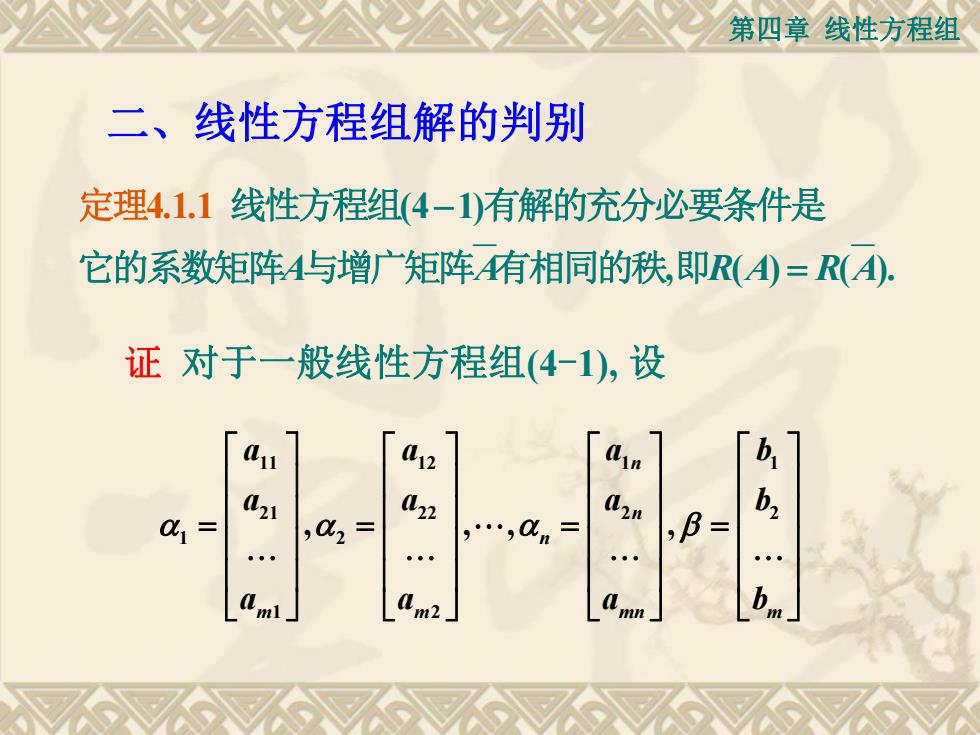
第四章 线性方程组 二、线性方程组解的判别 4.1.1 (4 1) A A , R(A) R(A).   线性方程组 有解的充分必要条件是 它的系数矩阵 与增广矩阵 有相同的秩 即 定理 证 对于一般线性方程组(4-1), 设 11 12 1 1 21 22 2 2 1 2 1 2 , , , , n n n m m mn m a a a b a a a b a a a b                                                           

第四章线性方程组 则线性方程组(4-1)可写为 1C1+x2C2+.+xnan=B(4-3) 并且 A=[aa,.an] A=[aa.an] 必要性 若方程组有解，则(4-3)知B可由a,a2,an线性 表示，于是向量组a1,c2,an与向量组C,2,Cn,月 等价.由性质2.3.1知秩{a1,a2,an}=秩{ag1,C2,an,] 所以R(A)=R(A):

第四章 线性方程组 则线性方程组(4-1)可写为 1 1 2 2 (4 3) n n x   x     x     1 2 1 2 n n A A                  并且 1 2 1 2 1 2 1 2 1 2 (4 3) , , , , , , , , , , . 2.3.1 , , , , , , ( ) ( ). n n n n n R A R A                          若方程组有解，则由 知 可由 线性 表示，于是向量组 与向量组 等价由性质 知秩{ }=秩{ , }, 所以 必要性