
中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 3、样本回归函数(SRF) 样本回归线: 对于X的一定值,取得Y的样本观测值,可计算其条件均 值,样本观测值条件均值的轨迹称为样本回归线。 样本回归函数: 如果把应变量Y的样本条件均值表示为解释变量X的某种 函数,这个函数称为样本回归函数(SRF)
3、样本回归函数(SRF) • X 样本回归线: 对于 的一定值,取得 的样本观测值,可计算其条件均 值,样本观测值条件均值的轨迹称为样本回归线。 样本回归函数: 如果把应变量 的样本条件均值表示为解释变量 的某种 函数,这个函数称为样本回归函数(SRF)。 • • • • X Y Y Y X

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 4.引入随机扰动项的原因 ◆代表未知的影响因素 ◆无法取得已知影响因素的代表指标 ◆众多细小影响因素的综合影响 ◆模型的设定误差 ◆变量的观测误差 ◆变量内在随机性
◆ 代表未知的影响因素 ◆ 无法取得已知影响因素的代表指标 ◆ 众多细小影响因素的综合影响 ◆ 模型的设定误差 ◆ 变量的观测误差 ◆ 变量内在随机性 4.引入随机扰动项的原因

中面寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 5.“线性”的理解: E(Y X)=B+BX 变量、参数均为“线性” E(Y X)=B+BX2 参数“线性”,变量”非线性” E(YX)=B+√B,X,变量“线性”,参数”非线性” 计量经济学中: 线性回归模型主要指就参数而言是“线性”,因为只要对 参数而言是线性的,都可以用类似的方法估计其参数
变量、参数均为“线性” 参数“线性”,变量”非线性” 变量“线性”,参数”非线性” 计量经济学中: 线性回归模型主要指就参数而言是“线性”,因为只要对 参数而言是线性的,都可以用类似的方法估计其参数。 E( ) Y X X i i i = + 1 2 2 E( ) Y X X i i i = + 1 2 E( ) Y X X i i i = + 1 2 5. “线性”的理解:
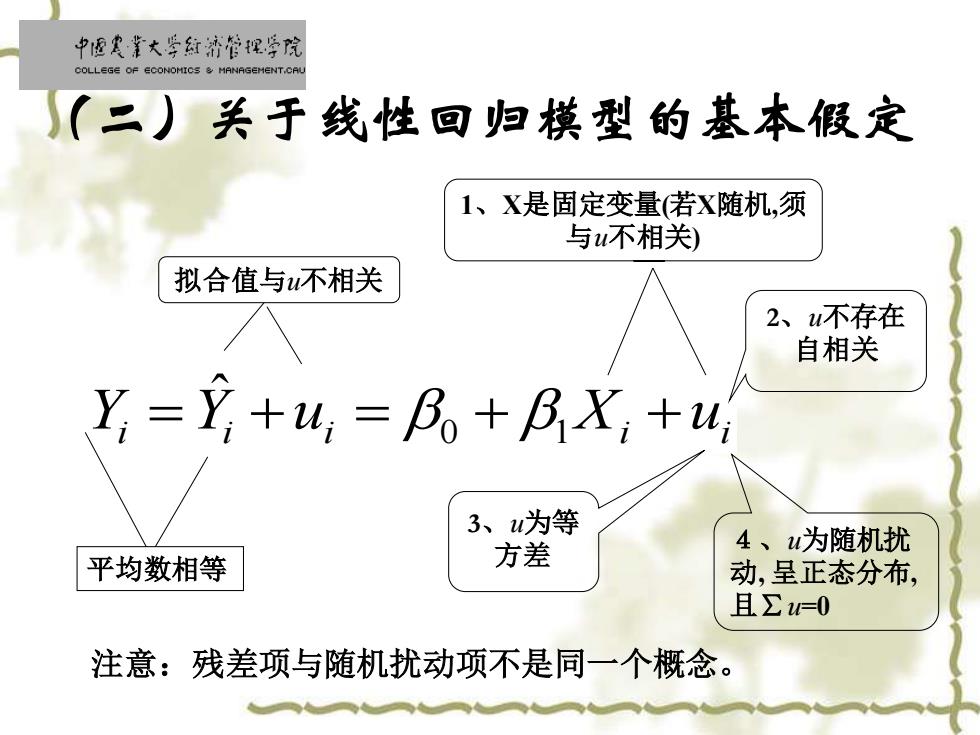
中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (二)关于线性回归模型的基本假定 1、X是固定变量若x随机,须 与不相关) 拟合值与u不相关 2、不存在 自相关 Y=Y+w,=B。+BX,+u 3、u为等 4、u为随机扰 平均数相等 方差 动,呈正态分布, 且∑u=0 注意:残差项与随机扰动项不是同一个概念
(二)关于线性回归模型的基本假定 Yi =Yi +ui = 0 + 1 Xi +ui ˆ 4、u为随机扰 动, 呈正态分布, 且∑u=0 平均数相等 拟合值与u不相关 1、X是固定变量(若X随机,须 与u不相关) 注意:残差项与随机扰动项不是同一个概念。 2、u不存在 自相关 3、u为等 方差
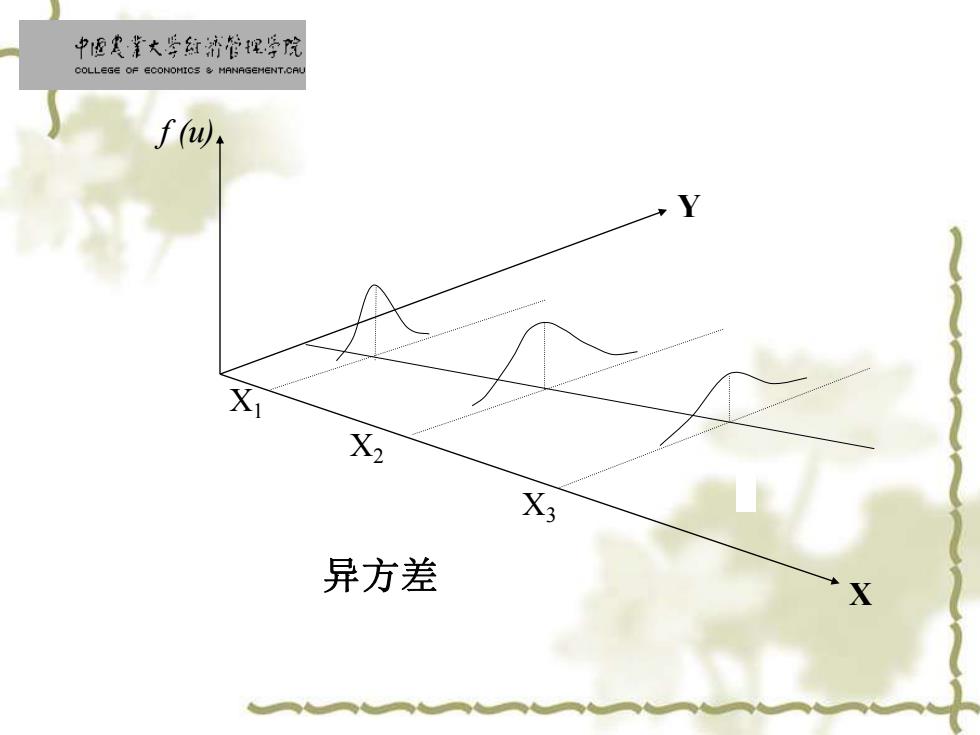
中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL f( X2 X3 异方差 X
f (u) Y X 3 X 2 X 1 异方差 X