
第七章 有相关(Autocorrelation)
第七章 自相关(Autocorrelation)

主要内容 一、自相关的会义和类型 二、自相关的来源及后果 三、自相关的检验 四、消除自相关和估计模型 五、EViews的应用 六、案例
主要内容 一、自相关的含义和类型 二、自相关的来源及后果 三、自相关的检验 四、消除自相关和估计模型 五、EViews的应用 六、案例

、自相关的会义和类型 1、含义: (1)简化协方差Cov(u,u)≠0(i≠j) 假定:Cov(u,us)=Cov(uus)) E(uu)=E(uu) to=E(u:u)=o2 =E(uu)=E(uu) 2=E(u:U2)=E(u:u2) I=E(utus)=E(uu+s)
1、含义: (1)简化协方差 (u u ) 0 (i j) Cov i j r (u u ) (u u ) r (u u ) (u u ) r (u u ) (u u ) r (u u ) E(u u ) E(u u ) Cov(u u ) Cov(u u ) s t t-s t t s 2 t t-2 t t 2 1 t t-1 t t 1 2 0 t t t t-1 t t 1 t t-s t t s + + + + + = = = = = = = = = = E E E E E E E u 假定: 一、自相关的含义和类型

(2)自相关集数 p: Cov(u,uts) E(uus) Var(u,)Var(u-) VE(4)E() E(4,4s= 10 0 =%P1 r2=10P2 、=%P
(2) 自相关系数 s s t s t t s t t t s t s r r r r r r r r r E u u E u E u E u u Var u u Cov u u ( ) ( ) ( ) ( ) ( ) Var( ) ( ) 0 2 0 2 1 0 1 0 0 t-s 2 2 t-s t-s = = = = = = = − −
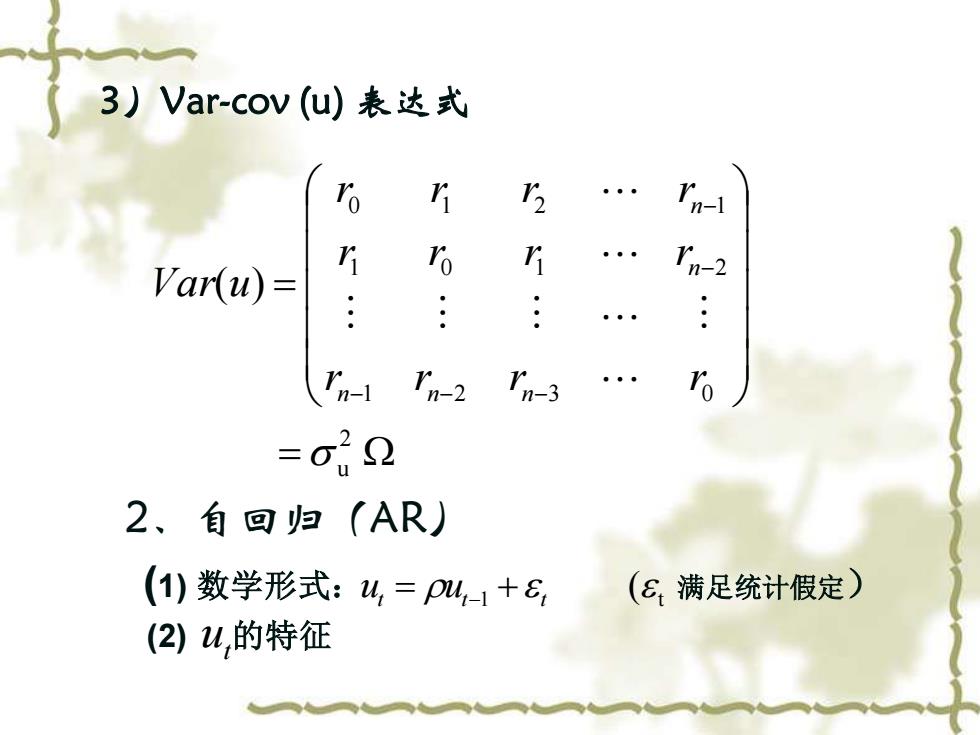
3)Var-cov(u)表达式 r n-1 i o r Var(u)= In-2 : : n- In-2 In-3 =o22 2、自回归(AR) (1)数学形式:4,=p4,1+ (E满足统计假定) (2)u,的特征
3)Var-cov (u) 表达式 = = − − − − − ( ) 2 u 1 2 3 0 1 0 1 2 0 1 2 1 r r r r r r r r r r r r Var u n n n n n 2、自回归(AR) (1) 数学形式: 满足统计假定) (2) 的特征 ( 1 t t t t u = u − + t u