
第四章多重共线性 一、填空题 1.在多元线性回归模型中,解释变量问呈现近似线性关系的现象为问题,给 计量经济建模带来不利影响,因此需检验和处理它。 2.在回归分析中,当检验回归系数所得的t值不显著时,我们往往将它归结为多重共 线性。但也可能是其他原因的影响,如 或 3.存在多重共线时,回归系数的标准差趋于 ,t值趋于 。方差膨胀 因子越大,OLS估计量的将越大。 4.检验样本是否存在多重共线性的常见方法有:】 和 5.处理多重共线性的方法主要有两大类:_ 和 二、问答题 1.简述多重共线性的含义。 2.简述多重共线性的后果 3.方差膨胀因子(Variance Inflation Factor,VIF)及其含义? 4.列举多重共线性的检验方法。 5.多重共线性的补救办法? 6.假设在模型y=风%+AX山+X2+叫,中,:与X2之间的相关系数为零,于是有人 建议你进行如下回归 Y;=ao+aXu+uu Yi=Y0+Y2X2i+uzi ()是否存在云=月且2=历?为什么? (2)0会等于0或0或某两个的某个线性组合吗?
第四章 多重共线性 一、填空题 1. 在多元线性回归模型中,解释变量间呈现近似线性关系的现象为_问题,给 计量经济建模带来不利影响,因此需检验和处理它。 2. 在回归分析中,当检验回归系数所得的 t 值不显著时,我们往往将它归结为多重共 线性。但也可能是其他原因的影响,如 或 。 3. 存在多重共线时,回归系数的标准差趋于 ,t 值趋于 。方差膨胀 因子越大,OLS 估计量的 将越大。 4. 检验样本是否存在多重共线性的常见方法有:_ 、 和 。 5. 处理多重共线性的方法主要有两大类:_和_。 二、问答题 1. 简述多重共线性的含义。 2. 简述多重共线性的后果。 3. 方差膨胀因子(Variance Inflation Factor, VIF)及其含义? 4. 列举多重共线性的检验方法。 5. 多重共线性的补救办法? 6. 假设在模型 Yi = 0 + 1X1i + 2X2i + ui 中, X1 与 X 2 之间的相关系数为零,于是有人 建议你进行如下回归: i i i i i i Y X u Y X u 0 2 2 2 0 1 1 1 = + + = + + (1) 是否存在 1 1 ˆ ˆ = 且 2 2 ˆ ˆ = ?为什么? (2) 0 ˆ 会等于 0 ˆ 或 0 ˆ 或某两个的某个线性组合吗?

(B)是否有vaa)=var)且val2)=var2)? 7.在决定一个回归模型的最优解释变量集时人们常用逐步回归的方法。在逐步回归 中既可采取每次引进一个解释变量的程序逐步向前回归),也可以先把所有可能的解释变量 都放在一个多元回归中,然后逐一地将它们除逐步向后回归)加进或别除一个变量,通 常是根据F检验看其对ES$的贡献而作出决定的。根据你现在对多重共线性的认识,你赞 成任何一种逐步回归的程序吗?为什么? 8.克莱因与戈德伯格曾用1921-1950年1942-194年战净期间略去)美国国内消费Y和 工资收入X1、非工资一非农业收入X2、农业收入X3的时间序列资料,利用OLSE估计得 出了下列回归方程 Y=8.133+1.059X1+0.452X2+0.121X3 (8.92)(0.17) (0.66)(1.09) R2=0.95F=107.37 括号中的数据为相应参数估计量的标准误。试对上述模型进行评析,指出其中存在的问题。 9.将下列函数以适当的方法消除多重共线性 (1)消费函数为:C=%+BW+2P+u,式中C、W、P分别表示消费、工资收入 和啡工资收入,W与P可能高度相关,但研究表明B2=月2。 (2)需求函数为:Q=%+AY+P+房P+u,式中Q、Y、P、P分别表示需求量、 收入水平、该商品价格及其替代品价格水平,P、P,可能高度相关。 三、实践题 L.下表给出了中国商品进口额Y、国内生产总值GDP、消费者价格指数CPI 商品进口额国内生产总值 年份 居民消费价格指数 (亿元) (亿元) (1985=100) 19851257.8 8964.4 100
(3) 是否有 ( ) ( ) 1 1 var ˆ ˆ var = 且 ( ) ( ) 2 2 var ˆ ˆ var = ? 7. 在决定一个回归模型的“最优”解释变量集时人们常用逐步回归的方法。在逐步回归 中既可采取每次引进一个解释变量的程序(逐步向前回归),也可以先把所有可能的解释变量 都放在一个多元回归中,然后逐一地将它们剔除(逐步向后回归)。加进或剔除一个变量,通 常是根据 F 检验看其对 ESS 的贡献而作出决定的。根据你现在对多重共线性的认识,你赞 成任何一种逐步回归的程序吗?为什么? 8.克莱因与戈德伯格曾用 1921-1950 年(1942-1944 年战争期间略去)美国国内消费 Y 和 工资收入 X1、非工资—非农业收入 X2、农业收入 X3 的时间序列资料,利用 OLSE 估计得 出了下列回归方程: 0.9 5 107.3 7 (8.92) (0.17) (0.66) (1.09) 8.133 1.059 0.452 0.121 ˆ 2 1 2 3 = = = + + + R F Y X X X 括号中的数据为相应参数估计量的标准误。试对上述模型进行评析,指出其中存在的问题。 9. 将下列函数以适当的方法消除多重共线性 (1)消费函数为: C = 0 + 1W + 2P+u ,式中 C、W、P 分别表示消费、工资收入 和非工资收入,W 与 P 可能高度相关,但研究表明 1 / 2 2 = 。 (2)需求函数为: Q = 0 + 1 Y + 2P+ 3Ps +u ,式中 Q、Y、P、Ps 分别表示需求量、 收入水平、该商品价格及其替代品价格水平,P、Ps 可能高度相关。 三、实践题 1. 下表给出了中国商品进口额 Y、国内生产总值 GDP、消费者价格指数 CPI。 年份 商品进口额 (亿元) 国内生产总值 (亿元) 居民消费价格指数 (1985=100) 1985 1257.8 8964.4 100
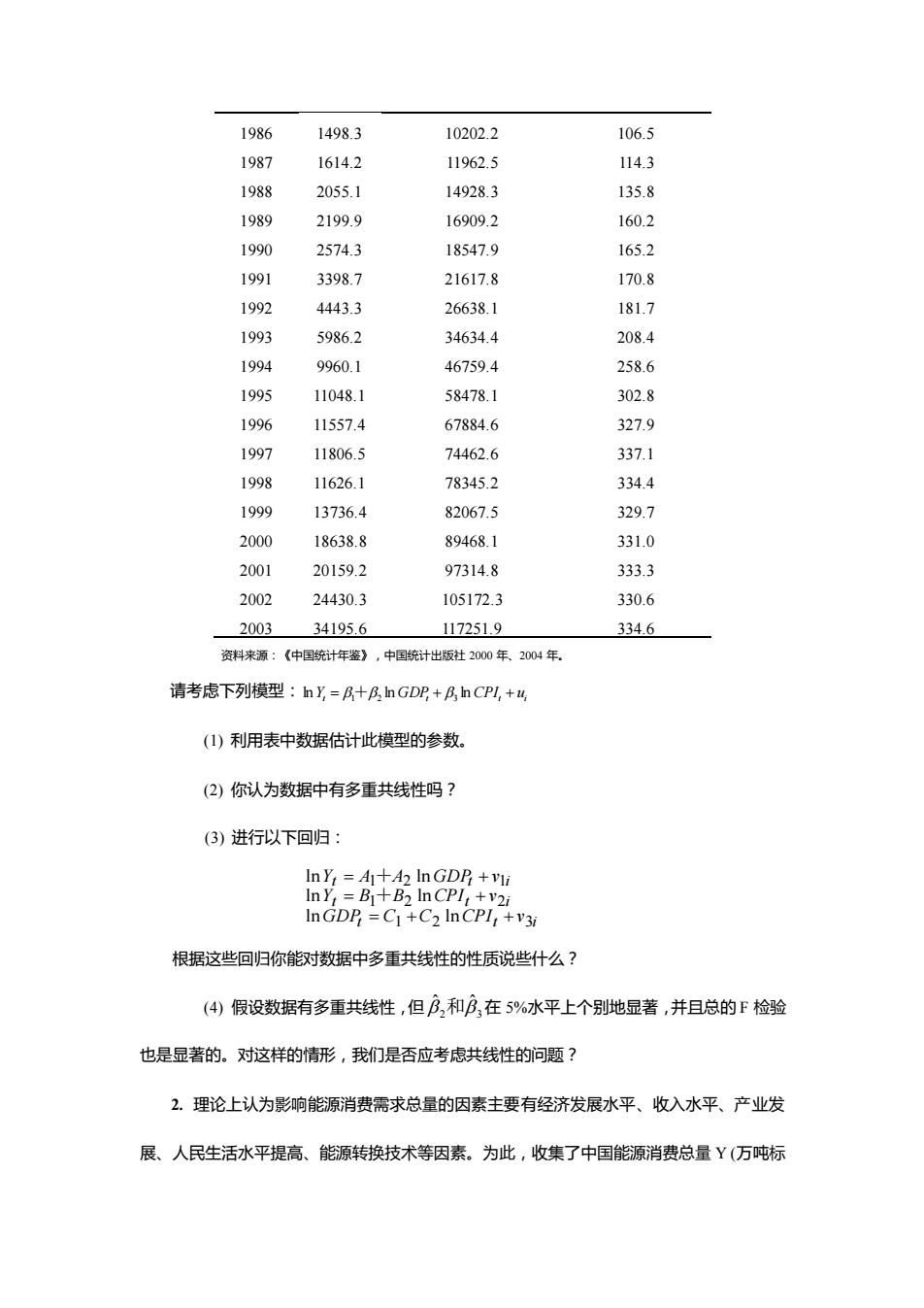
1986 1498.3 10202.2 106.5 1987 1614.2 11962.5 114.3 1988 2055.1 14928.3 135.8 1989 2199.9 16909.2 160.2 1990 2574.3 18547.9 165.2 1991 3398.7 21617.8 170.8 1992 4443.3 26638.1 181.7 1993 5986.2 34634.4 208.4 1994 9960.1 46759.4 258.6 1995 11048.1 58478.1 302.8 1996 11557.4 67884.6 327.9 1997 11806.5 74462.6 337.1 1998 11626.1 78345.2 334.4 1999 13736.4 82067.5 329.7 2000 18638.8 894681 331.0 2001 20159.2 97314.8 333.3 2002 24430.3 105172.3 330.6 2003 34195.6 17251.9 334.6 资料来源:《中国统计年要),中回统计世版社2000年、2004年. 请考虑下列模型:ny=R+民,hGDP+B,hn CPI,+码 (1)利用表中数据估计此模型的参数。 (2)你认为数据中有多重共线性吗? (3)进行以下回归: In Y:=A1+A2 In GDP +vu 根据这些回归你能对数据中多重共线性的性质说些什么? (4假设数据有多重共线性,但,和B,在5%水平上个别地显著,并且总的F检验 也是显著的。对这样的情形,我们是否应考虑共线性的问题? 2.理论上认为影响能源消费需求总量的因素主要有经济发展水平、收入水平、产业发 展、人民生活水平提高、能源转换技术等因素。为此,收集了中国能源消费总量Y(万吨标
1986 1498.3 10202.2 106.5 1987 1614.2 11962.5 114.3 1988 2055.1 14928.3 135.8 1989 2199.9 16909.2 160.2 1990 2574.3 18547.9 165.2 1991 3398.7 21617.8 170.8 1992 4443.3 26638.1 181.7 1993 5986.2 34634.4 208.4 1994 9960.1 46759.4 258.6 1995 11048.1 58478.1 302.8 1996 11557.4 67884.6 327.9 1997 11806.5 74462.6 337.1 1998 11626.1 78345.2 334.4 1999 13736.4 82067.5 329.7 2000 18638.8 89468.1 331.0 2001 20159.2 97314.8 333.3 2002 24430.3 105172.3 330.6 2003 34195.6 117251.9 334.6 资料来源:《中国统计年鉴》,中国统计出版社 2000 年、2004 年。 请考虑下列模型: Yt = GDPt + CPIt + ui ln 1+2 ln 3 ln (1) 利用表中数据估计此模型的参数。 (2) 你认为数据中有多重共线性吗? (3) 进行以下回归: t t i t t i t t i GDP C C CPI v Y B B CPI v Y A A GDP v 1 2 3 1 2 2 1 2 1 ln ln ln ln ln ln = + + = + = + + + 根据这些回归你能对数据中多重共线性的性质说些什么? (4) 假设数据有多重共线性,但 2 3 ˆ 和 ˆ 在 5%水平上个别地显著,并且总的 F 检验 也是显著的。对这样的情形,我们是否应考虑共线性的问题? 2. 理论上认为影响能源消费需求总量的因素主要有经济发展水平、收入水平、产业发 展、人民生活水平提高、能源转换技术等因素。为此,收集了中国能源消费总量 Y (万吨标
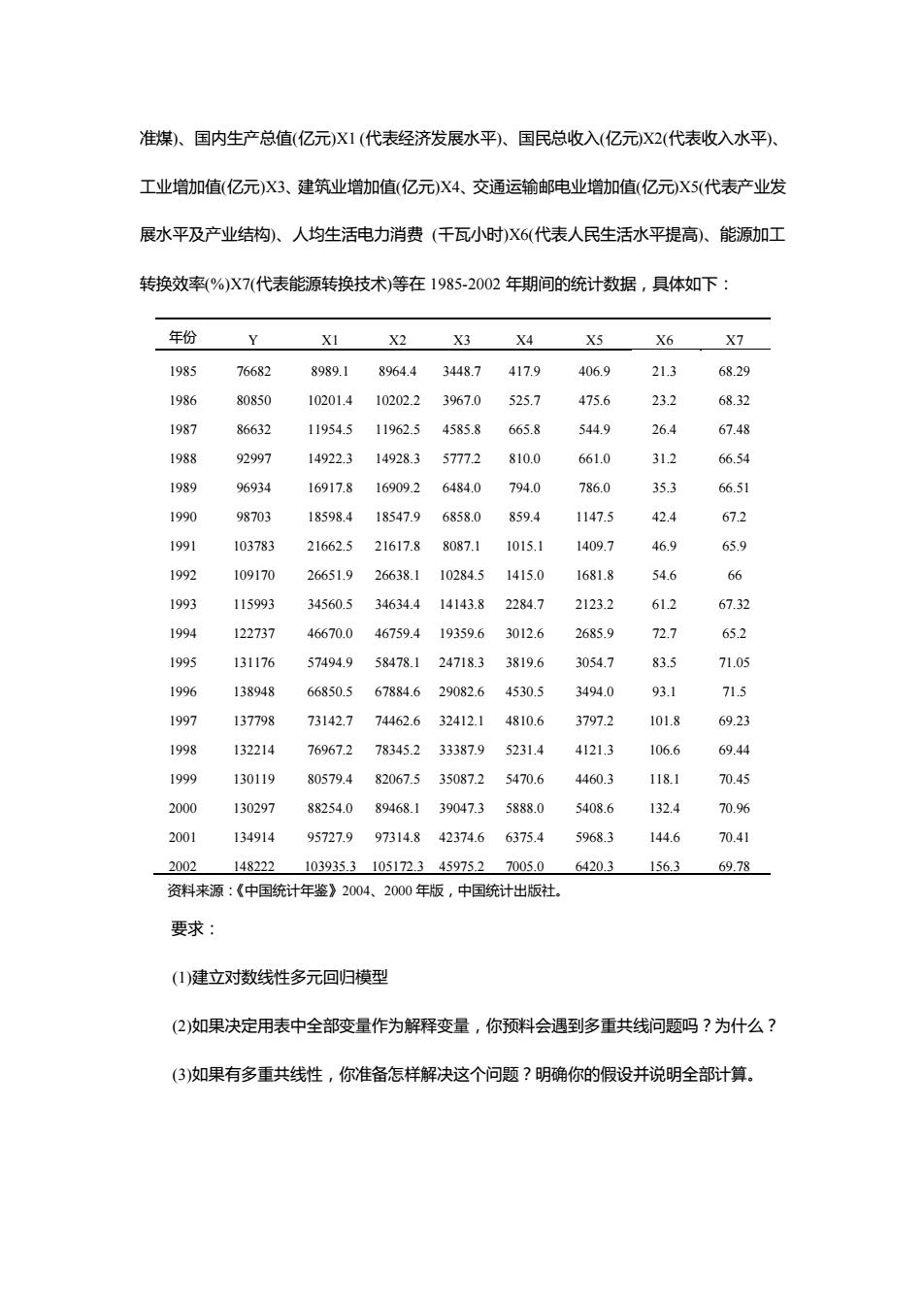
准煤,、国内生产总值(亿元)X1(代表经济发展水平)、国民总收入(亿元X2(代表收入水平)】 工业增加值(亿元)X3、建筑业增加值(亿元)X4、交通运输邮电业增加值(亿元X5(代表产业发 展水平及产业结构)、人均生活电力消费(千瓦小时)X6(代表人民生活水平提高)、能源加工 转换效率(%)X7(代表能源转换技术)等在1985-2002年期间的统计数据,具体如下 年份 X2 X3 X4 X5 X7 1985 76682 8989.18964.43448.7417.9 406.9 213 68.29 1986 80850 10201.410202.23967.0525.7 475.6 232 68.32 1987 86632 11954.5 11962.5 4585.8 665.8 5449 26.4 67.48 1988 92997 14922.314928357772 810.0 661.0 312 6.54 1989 96934 16917.8 16909.26484.0 794.0 786.0 353 66.51 190 98703 185984 18547.9 6858.0 859.4 1147.5 424 672 1991 103783 21662.521617.88087.1 1015.1 1409.7 46.9 659 1992 109170 26651.9 26638.1 10284.5 1415.0 1681.8 54.6 1993 115993 34560.5346344141438 2284.7 2123,2 612 67.32 1994 122737 46670.0 46759.419359.6 3012.6 2685.9 72.7 652 1995 131176 57494.9 58478.1 247183 3819.6 3054.7 835 71.0 1996 138948 66850.567884.6290826 4530.5 3494.0 931 1997 137798 73142.7 74462.632412.1 4810.6 3797.2 101.8 69.23 1998 13214 769672 78345,2 33387.9 52314 41213 106.6 694 1999 130119 80579.482067.535087.25470.6 4460.3 118.1 70.45 2000 130297 88254.089468.13904735888.0 5408.6 132.4 70.9% 2001 134914 95727.997314.842374.663754 5968.3 144.6 70.41 2002 148222103935.3105172.345975.27005.06420.3 156.3 69.78 资抖来源:《中国统计年鉴》2004.2000年版,中国统计出饭社. 要求 (1)建立对数线性多元回归模型 2如果决定用表中全部变量作为解释变量,你预料会遇到多重共线问题吗?为什么? (3)如果有多重共线性,你准备怎样解决这个问题?明确你的假设并说明全部计算
准煤)、国内生产总值(亿元)X1 (代表经济发展水平)、国民总收入(亿元)X2(代表收入水平)、 工业增加值(亿元)X3、建筑业增加值(亿元)X4、交通运输邮电业增加值(亿元)X5(代表产业发 展水平及产业结构)、人均生活电力消费 (千瓦小时)X6(代表人民生活水平提高)、能源加工 转换效率(%)X7(代表能源转换技术)等在 1985-2002 年期间的统计数据,具体如下: 年份 Y X1 X2 X3 X4 X5 X6 X7 1985 76682 8989.1 8964.4 3448.7 417.9 406.9 21.3 68.29 1986 80850 10201.4 10202.2 3967.0 525.7 475.6 23.2 68.32 1987 86632 11954.5 11962.5 4585.8 665.8 544.9 26.4 67.48 1988 92997 14922.3 14928.3 5777.2 810.0 661.0 31.2 66.54 1989 96934 16917.8 16909.2 6484.0 794.0 786.0 35.3 66.51 1990 98703 18598.4 18547.9 6858.0 859.4 1147.5 42.4 67.2 1991 103783 21662.5 21617.8 8087.1 1015.1 1409.7 46.9 65.9 1992 109170 26651.9 26638.1 10284.5 1415.0 1681.8 54.6 66 1993 115993 34560.5 34634.4 14143.8 2284.7 2123.2 61.2 67.32 1994 122737 46670.0 46759.4 19359.6 3012.6 2685.9 72.7 65.2 1995 131176 57494.9 58478.1 24718.3 3819.6 3054.7 83.5 71.05 1996 138948 66850.5 67884.6 29082.6 4530.5 3494.0 93.1 71.5 1997 137798 73142.7 74462.6 32412.1 4810.6 3797.2 101.8 69.23 1998 132214 76967.2 78345.2 33387.9 5231.4 4121.3 106.6 69.44 1999 130119 80579.4 82067.5 35087.2 5470.6 4460.3 118.1 70.45 2000 130297 88254.0 89468.1 39047.3 5888.0 5408.6 132.4 70.96 2001 134914 95727.9 97314.8 42374.6 6375.4 5968.3 144.6 70.41 2002 148222 103935.3 105172.3 45975.2 7005.0 6420.3 156.3 69.78 资料来源:《中国统计年鉴》2004、2000 年版,中国统计出版社。 要求: (1)建立对数线性多元回归模型 (2)如果决定用表中全部变量作为解释变量,你预料会遇到多重共线问题吗?为什么? (3)如果有多重共线性,你准备怎样解决这个问题?明确你的假设并说明全部计算

参考答案 一、填空题 1.多重共线性;2.设定偏误;模型的理论依据不强。3.无穷大;很小;标准差。4.简单相 关系数;可决系数法;参数t检验的显著性。5.差分法;逐步回归法。 二、问答题 1.答:对于K元线性回归模型 y=月。+月Xn+BX2+.+BX+4,-l,2,n 其基本假设之一是解释变量之间是互相独立的.如果某两个或多个解释变量之间出现了 相关性,则称为多重共线性。如果存在 2X4+23X2+.+Xk=0, =1,2.,n 其中,不全为0,即某一个解释变量可以用其它解释变量的线性组合表示,则称为完全 共线性。 2.答:在多重共线性存在的情况下,OLS估计量仍然保持BLUE的性质。虽然OLS估 计量可以得到,但极不稳定,数据资料即使有极小的变化,估计值及标准差就会有很敏感的 反应。估计量的方差随着共线程度的增加而变大,如果达到完全共线,估计量的方差就会为 无限大。随着共线程度的增加,对于回归系数所进行的t检验,接受原假设的概率加大,即 回归系数可能变得不显著。但与此同时,可以得到较高的可决系数(),如果模型的用途 是预测,那么,高度的多重共线未必不是好事。 3.答:回归系数的OLS估计量的方差为:Var(b)=o(XX),可以看作随机项方 差σ乘上一个比例常数(XX),这个比例常数称为方差膨胀因子,即 VIF=X) 可以证明:
参考答案 一、填空题 1.多重共线性;2.设定偏误;模型的理论依据不强。3. 无穷大;很小;标准差。4.简单相 关系数;可决系数法;参数 t 检验的显著性。5. 差分法;逐步回归法。 二、问答题 1. 答:对于 K 元线性回归模型 Yi = 0 + 1Xi1 + 2Xi2 ++ k Xik + ui , i=1,2,.,n 其基本假设之一是解释变量之间是互相独立的。如果某两个或多个解释变量之间出现了 相关性,则称为多重共线性。如果存在 1Xi1 + 2Xi2 ++ k Xik = 0 , i=1,2,.,n 其中不全为 0,即某一个解释变量可以用其它解释变量的线性组合表示,则称为完全 共线性。 2. 答:在多重共线性存在的情况下,OLS 估计量仍然保持 BLUE 的性质。虽然 OLS 估 计量可以得到,但极不稳定,数据资料即使有极小的变化,估计值及标准差就会有很敏感的 反应。估计量的方差随着共线程度的增加而变大,如果达到完全共线,估计量的方差就会为 无限大。随着共线程度的增加,对于回归系数所进行的 t 检验,接受原假设的概率加大,即 回归系数可能变得不显著。但与此同时,可以得到较高的可决系数(R 2),如果模型的用途 是预测,那么,高度的多重共线未必不是好事。 3. 答:回归系数的 OLS 估计量的方差为: 2 1 ( ) ( ) − = Var b u X X ii ,可以看作随机项方 差 2 u 乘上一个比例常数 1 ( ) − X X ii ,这个比例常数称为方差膨胀因子,即 1 ( ) − = VIFi X X ii 可以证明: