
中虚寒笔大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 使用相关华数时应注意 ◆X和Y都是相互对称的随机变量; ◆线性相关系数只反映变量间的线性相关程度,不能说明 非线性相关关系; ◆样本相关系数是总体相关系数的样本估计值,因抽样 波动,样本相关系数为随机变量,其统计显著性有待检验; ◆相关系数只能反映线性相关程度,不能确定因果关系,不 能说明相关关系具体接近娜条直线。 计量经济学关心:变量间的因果关系及隐藏在随机性后 面的统计规律性,这有赖于回归分析方法
◆ 和 都是相互对称的随机变量; ◆线性相关系数只反映变量间的线性相关程度,不能说明 非线性相关关系; ◆样本相关系数是总体相关系数的样本估计值,因抽样 波动,样本相关系数为随机变量,其统计显著性有待检验; ◆相关系数只能反映线性相关程度,不能确定因果关系,不 能说明相关关系具体接近哪条直线. 计量经济学关心:变量间的因果关系及隐藏在随机性后 面的统计规律性,这有赖于回归分析方法. 使用相关系数时应注意 X Y

中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 4.回归分析 ◆ 回归的古典意义: 道尔顿遗传学的回归概念:父母身高与子女 身高的关系。 ◆回归的现代意义: 一个因变量对若干解释变量依存关系的研究。 ◆回归的目的(实质): 由固定的解释变量去估计因变量的平均值
◆ 回归的古典意义: 道尔顿遗传学的回归概念: 父母身高与子女 身高的关系。 ◆ 回归的现代意义: 一个因变量对若干解释变量依存关系的研究。 ◆ 回归的目的(实质): 由固定的解释变量去估计因变量的平均值。 4.回归分析

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (二)一元线性回归模型 1.一元线性回归模型设定 一元线性总体回归模型:Y=B。+B,X+u 一元线性总体回归函数:E(YX)=B+BX (Population Regression Function,PRF) 一元线性样本回归模型:Y=b,+b,X+e 一元线性样本回归函数:E(YX)=b,+bX (Sample Regression Function,SRF) 实际的经济研究中总体回归函数通常是未知的,只能根 据经济理论和实践经验去设定。“计量”的目的就是寻求 样本回归函数作为总体回归函数的估计
(二)一元线性回归模型 E(Y X) = 0 + 1 X Y = 0 + 1 X +u Y = b +b X + e 0 1 一元线性总体回归模型: 一元线性总体回归函数: (Population Regression Function, PRF) 一元线性样本回归模型: 一元线性样本回归函数: (Sample Regression Function, SRF) E(Y X) = b0 +b1 X 实际的经济研究中总体回归函数通常是未知的,只能根 据经济理论和实践经验去设定。“计量”的目的就是寻求 样本回归函数作为总体回归函数的估计。 1. 一元线性回归模型设定
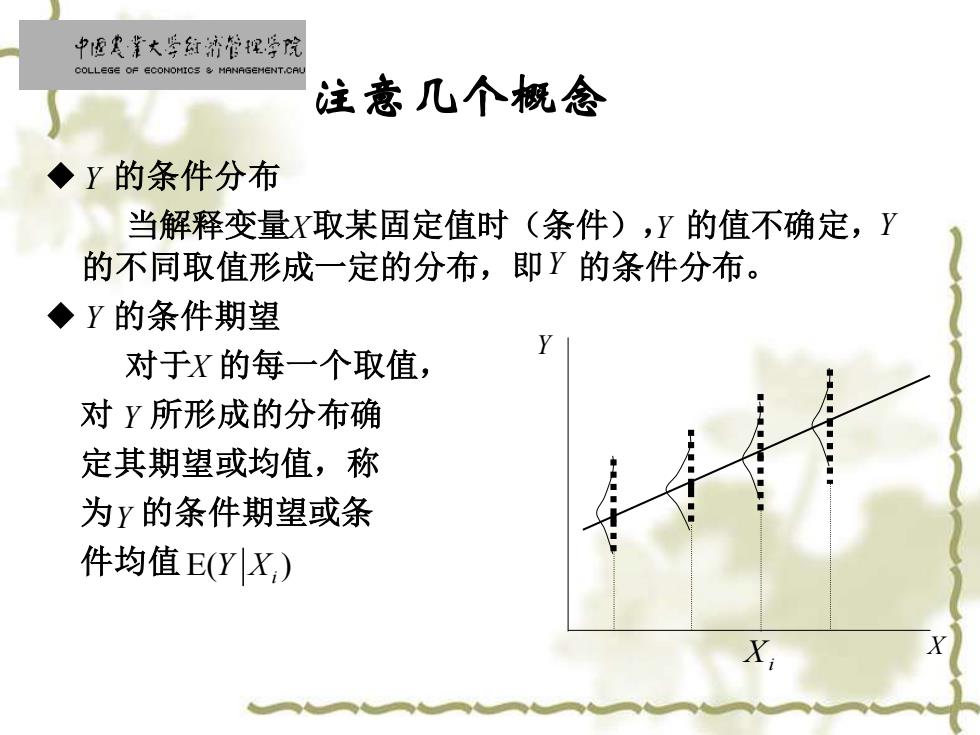
中慢寒靠大学红济管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 注意几个概念 ◆Y的条件分布 当解释变量X取某固定值时(条件),Y的值不确定,Y 的不同取值形成一定的分布,即Y的条件分布。 ◆Y的条件期望 对于X的每一个取值, 对Y所形成的分布确 定其期望或均值,称 为y的条件期望或条 件均值E(YX,)
◆ 的条件分布 当解释变量 取某固定值时(条件), 的值不确定, 的不同取值形成一定的分布,即 的条件分布。 ◆ 的条件期望 对于 的每一个取值, 对 所形成的分布确 定其期望或均值,称 为 的条件期望或条 件均值 注意几个概念 Xi X Y Y Y Y Y Y Y X Y X E( ) Y Xi
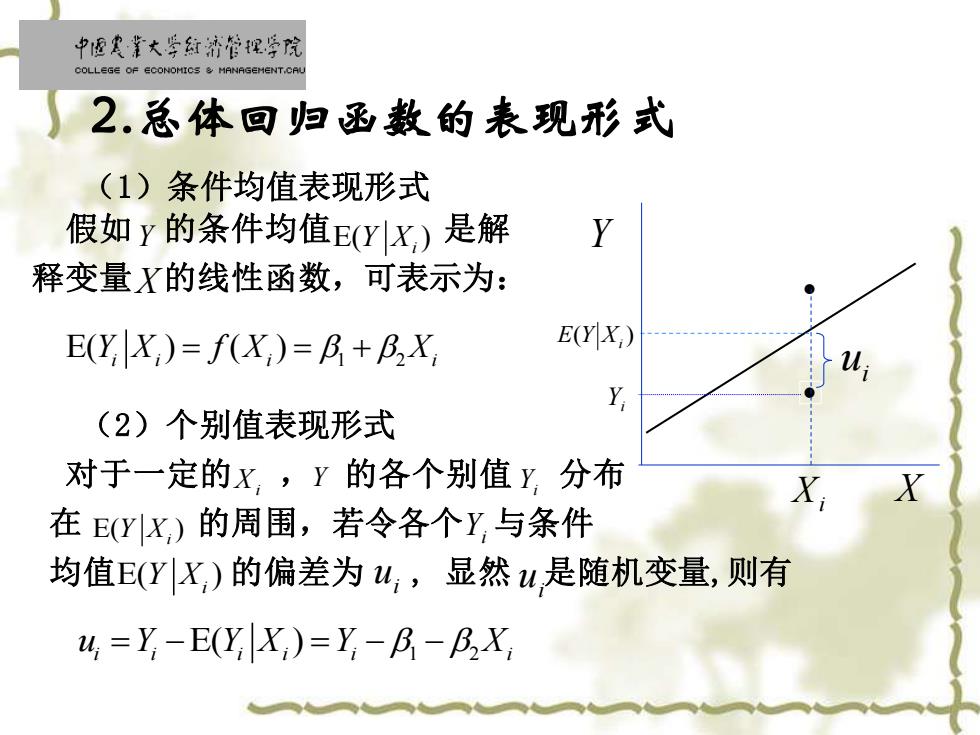
中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL )2.总体回归函数的表现形式 (1)条件均值表现形式 假如y的条件均值E(Yx)是解 释变量X的线性函数,可表示为: E(Y X)=f(X)=B+BX E(Y X,) (2)个别值表现形式 对于一定的x,y的各个别值y分布 X X 在EYx)的周围,若令各个Y,与条件 均值E(YX)的偏差为w,显然u,是随机变量,则有 u=Y-E(Y X)=Y-B-BX
• • i u Xi X Y ( ) E Y Xi Yi (1)条件均值表现形式 假如 的条件均值 是解 释变量 的线性函数,可表示为: (2)个别值表现形式 对于一定的 , 的各个别值 分布 在 的周围,若令各个 与条件 均值 的偏差为 , 显然 是随机变量,则有 2.总体回归函数的表现形式 Xi E( ) Y Xi E( ) ( ) Y X f X X i i i i = = + 1 2 Yi E( ) Y Xi Yi E( ) Y Xi i u i u i i i i i i E( ) 1 2 u Y Y X Y X = − = − − Y Y X