
第九章滞后变量模型 一单项选择题 1下列属于有限分布滞后模型的是(。 A.Y=a+box,+br+by2++u B.Y=a+bX,+bX,+.+w, C.Y.=a+box,+br+b2Y-2+.+by+u D.Y,=a+boX,+bx+b2X-2++b+u 2消费函数模型C,=400+0.5L,+0.31+0.1山-2,其中1为收入,则当期收入1。 对未来消费C2的影响是:I增加1单位,C2增加( A.0.5单位 B.0.3单位 C0.1单位 D.0.9单位 3在分布滞后模型y,=a+bX,+bX,+b2X,2+.+bX,-t+山,中,长期乘数 为 A.bo B.b(i=1,2,k) CXA D. 4.在分布滞后模型的估计中,使用时间序列资料可能存在的序列相关问题就表现为 ( A异方差问题 B.自相关问题 C.多重共线性问题 D.随机解释变量问题
第九章 滞后变量模型 一. 单项选择题 1.下列属于有限分布滞后模型的是( )。 A. Yt = +b0Xt +b1Yt−1 +b2Yt−2 ++ut B. Yt = + b0Xt + b1Xt−1 ++ ut C. Yt = + b0Xt + b1Yt−1 + b2Yt−2 ++ bkYt−k + ut D. Yt = + b0Xt + b1Xt−1 + b2Xt−2 ++ bk Xt−k + ut 2.消费函数模型 1 1 2 400 0.5 0.3 0. ˆ t = + t + t− + t− C I I I ,其中 I 为收入,则当期收入 It 对未来消费 Ct+2 的影响是:I 增加 1 单位,Ct+2 增加( )。 A. 0.5 单位; B. 0.3 单位 C. 0.1 单位; D. 0.9 单位 3.在分布滞后模型 Yt = + b0 Xt + b1Xt−1 + b2 Xt−2 ++ bk Xt−k + ut 中,长期乘数 为( )。 A. 0 b B. i b (i=1,2,.,k) C. = k i i b 1 D. = k i i b 0 4.在分布滞后模型的估计中,使用时间序列资料可能存在的序列相关问题就表现为 ( )。 A.异方差问题 B.自相关问题 C.多重共线性问题 D.随机解释变量问题

5对于有限分布滞后模型y,=a+bX,+X+b,X2++b,X,4+4,中,如果其 参数b,(1,2,k)可以近似地用一个关于滞后长度i(=1,2.k)的多项式表示,则称 此模型为()。 A有限多项式滞后模型 B无限多项式滞后模型 C考伊克变换模型 D.自适应预期模型 6.自适应预期模型基于如下的理论假设:影响被解释变量Y,的因素不是X而是关于 X的预期X,且预期X形成的过程是X-X,=y(X,-X),其中0<Y<1,Y被 称为()。 A衰减率 B预期系数 C.调整因子 D.预期误差 7.当分布滞后模型的随机误差项满足线性模型假定时,下列哪一个模型可以用最小 二乘法来估计( A.Y=a+box,+bX+bx-2++bx+u B.y,=al-)+bX,+2Y-+4-u C.y,=b+bX,+(1-y)Y+4,-1-y)u D.Y,=b。+b1X,+(1-8)Y,-1+4, 8.下列哪个模型的一阶自相关问题可用DW检验( A有限多项式分布滞后模型 B.自适应预期模型 C.库伊克变换模型 D.局部调整模型 9.有限多项式分布滞后模型中,通过将原分布滞后模型中的参数表示为滞后期的有 限多项式,从而克服了原分布滞后模型估计中的()。 A异方差问题 B.序列相关问题:
5.对于有限分布滞后模型 t t t t k t k t Y = + b X + b X + b X + + b X + u 0 1 −1 2 −2 − 中,如果其 参数 i b (i=1,2,., k) 可以近似地用一个关于滞后长度 i (i=1,2,.,k) 的多项式表示,则称 此模型为( )。 A.有限多项式滞后模型 B.无限多项式滞后模型 C.考伊克变换模型 D.自适应预期模型 6.自适应预期模型基于如下的理论假设:影响被解释变量 Yt 的因素不是 Xt ,而是关于 X 的预期 * Xt+1 ,且预期 * Xt+1 形成的过程是 * Xt+1 - * Xt = ( ) * Xt − Xt+1 ,其中 0<γ<1,γ 被 称为( )。 A.衰减率 B.预期系数 C.调整因子 D.预期误差 7.当分布滞后模型的随机误差项满足线性模型假定时,下列哪一个模型可以用最小 二乘法来估计( )。 A. t t t t k t k t Y = +b X +b X +b X + +b X +u 0 1 −1 2 −2 − B. 0 1 1 (1 ) t = − + t + t− + t − t− Y b X Y u u C. 0 1 1 1 (1 ) (1 ) Yt = b + b Xt + − Yt− + ut − − ut− D. Yt =b0 + b1Xt + − Yt−1 + ut (1 ) 8.下列哪个模型的一阶自相关问题可用 DW 检验( )。 A.有限多项式分布滞后模型 B.自适应预期模型 C.库伊克变换模型 D.局部调整模型 9.有限多项式分布滞后模型中,通过将原分布滞后模型中的参数表示为滞后期 i 的有 限多项式,从而克服了原分布滞后模型估计中的( )。 A. 异方差问题; B. 序列相关问题;

C,多重共线性问题:D.因包含无穷多个参数从而不可能被估计的问题 10.分布滞后模型y,=a+b,X,+b,X,-+b,X,-2+bX,-+u,中,为了使模型的自 由度达到30,必须拥有多少年的观测资料(), A32B.33 C.34 D.35 二、名词解释 1.滞后变量: 2.滞后效应 3.多项式分布滞后模型 4短期乘数和长期乘数: 5.自回归分布滞后模型; 6.自回归模型 三、问答题 1滞后外生变量模型和滞后内生变量模型的概念是什么? 2滞后变量横型有哪几种类型?外生变量分布滞后模型使用0LS方法存在哪些问 题? 3被解释变量对于一个或者多个解释变量反应滞后的原因是什么?给出一些分布滞 后模型的例子, 4.叙述用阿尔蒙多项式法估计外生变量有限分布滞后模型的方法步骤,对多项式的 次数r有哪些限制,为什么?4.滞后变量模型的作用是什么? 5,有限分布滞后模型估计的困难是什么? 6.什么是经验加权估计法?常见的滞后结构类型有那几种? 7.经验加权估计法的优缺点、通常做法是什么?
C. 多重共线性问题; D. 因包含无穷多个参数从而不可能被估计的问题 10.分布滞后模型 Yt = + b0 Xt + b1Xt−1 + b2 Xt−2 + b3Xt−3 + ut 中,为了使模型的自 由度达到 30,必须拥有多少年的观测资料( )。 A.32 B.33 C.34 D.35 二、名词解释 1.滞后变量; 2.滞后效应; 3.多项式分布滞后模型 4.短期乘数和长期乘数; 5.自回归分布滞后模型; 6.自回归模型 三、问答题 1.滞后外生变量模型和滞后内生变量模型的概念是什么? 2.滞后变量模型有哪几种类型?外生变量分布滞后模型使用 OLS 方法存在哪些问 题? 3.被解释变量对于一个或者多个解释变量反应滞后的原因是什么?给出一些分布滞 后模型的例子。 4. 叙述用阿尔蒙多项式法估计外生变量有限分布滞后模型的方法步骤,对多项式的 次数 r 有哪些限制,为什么?4.滞后变量模型的作用是什么? 5.有限分布滞后模型估计的困难是什么? 6. 什么是经验加权估计法?常见的滞后结构类型有那几种? 7.经验加权估计法的优缺点、通常做法是什么?

8.什么是阿尔蒙估计法?其基本原理是什么? 9.阿尔蒙估计法多项式的次数如何确定?滞后期长度如何确定? 10.什么是考伊克变换?意义何在? 11.考伊克模型的特点是什么?缺陷是什么? 12.什么是预期模型?难点是什么?如何解决? 13,什么是自适应预期模型?它是如何解决预期模型难点的? 14.考伊克模型、自适应预期模型和局部调整模型有何异同?模型估计会存在哪些 困难?如何解决? 15.检验一阶自回归模型随机误差项是否存在自相关,为什么用德宾h检验而不用 DW检验? 16.什么是局部调整模型?什么是局部调整假设? 四、实验题 1.考察以下分布滞后横型 Y.=a+box,+bx+b2X-2+bX-3+bX+bsX-s+u 假如用2阶有限多项式变换估计这个模型后得 y,=0.85+0.50Zom+0.45Z.-0.10Z,+4, 式中: -2.Z-2石-2x (1)求原模型中各参数的估计值; (2)试估计X对Y的短期乘数、中期乘数和长期乘数。 2.对于下列估计模型
8.什么是阿尔蒙估计法?其基本原理是什么? 9.阿尔蒙估计法多项式的次数如何确定?滞后期长度如何确定? 10.什么是考伊克变换?意义何在? 11.考伊克模型的特点是什么?缺陷是什么? 12.什么是预期模型?难点是什么?如何解决? 13.什么是自适应预期模型?它是如何解决预期模型难点的? 14.考伊克模型、自适应预期模型和局部调整模型有何异同?模型估计会存在哪些 困难?如何解决? 15.检验一阶自回归模型随机误差项是否存在自相关,为什么用德宾 h 检验而不用 DW 检验? 16.什么是局部调整模型?什么是局部调整假设? 四、实验题 1.考察以下分布滞后模型: Yt = + b0Xt + b1Xt−1 + b2Xt−2 + b3Xt−3 + b4Xt−4 + b5Xt−5 + ut 假如用 2 阶有限多项式变换估计这个模型后得 t t t t t Y = + Z + Z − Z + u 0 1 2 0.85 0.50 0.45 0.10 式中: ; 3 0 0 = = − i Z t Xt i ; 3 0 1 = = − i t t i Z iX ; 3 0 2 2 = = − i t Xt i Z i (1)求原模型中各参数的估计值; (2)试估计 X 对 Y 的短期乘数、中期乘数和长期乘数。 2.对于下列估计模型:
投资函数:1,=120+0.6Y,+0.8Y,1+0.4Y-2+02Y- 消费函数:C,=280+0.58Y+0.12C 其中,I为投资、Y为收入、C为消费。试分别计算投资、消费的短期影响乘数和长期影 响乘数,并解释其经济含义 3.下表给出某地区1980-2001年固定资产投资(Y)与销售额(X)的资料(单位: 亿元). 某地区1970-1991年固定资产投资(y)与销售额(x)的资料 年份 Y 年份 Y 1980 36.99 52.805 1991 128.68 168.129 1981 33.60 55.906 1992 123.97 163.351 1982 35.42 63.027 1993 117.35 172.547 1983 42.35 72.931 1994 139.61 190.682 1984 52.48 84.790 1995 152.88 194.538 1985 53.66 86.589 1996 137.95 194.657 1986 58.53 98.797 1997 141.06 206.326 1987 67.48 113.201 1998 163.45 223.541 1988 78.13 126.905 1999 183.80 232.724 1989 95.13 143.936 2000 192.61 239.459 1990 112.60154.391 2001 182.81 235.142 试就下列模型,按照一定的处理方法估计模型参数,并解释模型的经济意义,检验 模型随机误差项的一阶自相关性。 ()设定模型:y=b。+bX,+4,运用局部调整假定。 (2)设定模型:y,=b,+bX,+4,运用自适应预期假定。 ()运用阿尔蒙多项式变换法,估计分布滞后模型
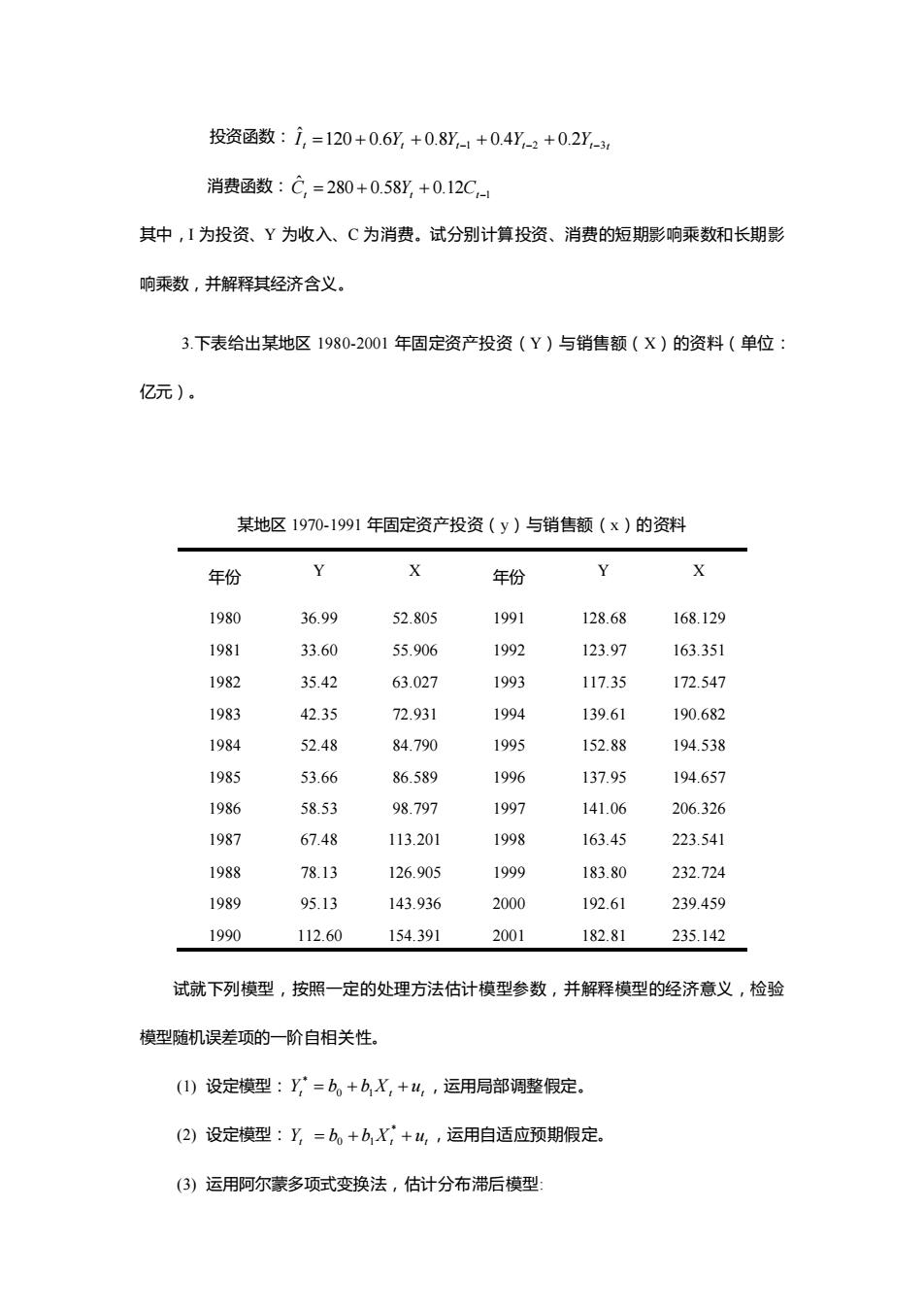
投资函数: t t t t t t I Y Y 1 Y 2 2Y 3 120 0.6 0.8 0.4 0. ˆ = + + − + − + − 消费函数: 12 1 280 0.58 0. ˆ Ct = + Yt + Ct− 其中,I 为投资、Y 为收入、C 为消费。试分别计算投资、消费的短期影响乘数和长期影 响乘数,并解释其经济含义。 3.下表给出某地区 1980-2001 年固定资产投资(Y)与销售额(X)的资料(单位: 亿元)。 某地区 1970-1991 年固定资产投资(y)与销售额(x)的资料 年份 Y X 年份 Y X 1980 36.99 52.805 1991 128.68 168.129 1981 33.60 55.906 1992 123.97 163.351 1982 35.42 63.027 1993 117.35 172.547 1983 42.35 72.931 1994 139.61 190.682 1984 52.48 84.790 1995 152.88 194.538 1985 53.66 86.589 1996 137.95 194.657 1986 58.53 98.797 1997 141.06 206.326 1987 67.48 113.201 1998 163.45 223.541 1988 78.13 126.905 1999 183.80 232.724 1989 95.13 143.936 2000 192.61 239.459 1990 112.60 154.391 2001 182.81 235.142 试就下列模型,按照一定的处理方法估计模型参数,并解释模型的经济意义,检验 模型随机误差项的一阶自相关性。 (1) 设定模型: Yt = b0 + b1Xt + ut * ,运用局部调整假定。 (2) 设定模型: Yt = b + b Xt + ut * 0 1 ,运用自适应预期假定。 (3) 运用阿尔蒙多项式变换法,估计分布滞后模型: