中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL f(以 X X2 氵=B。+BX X3 同方差 X
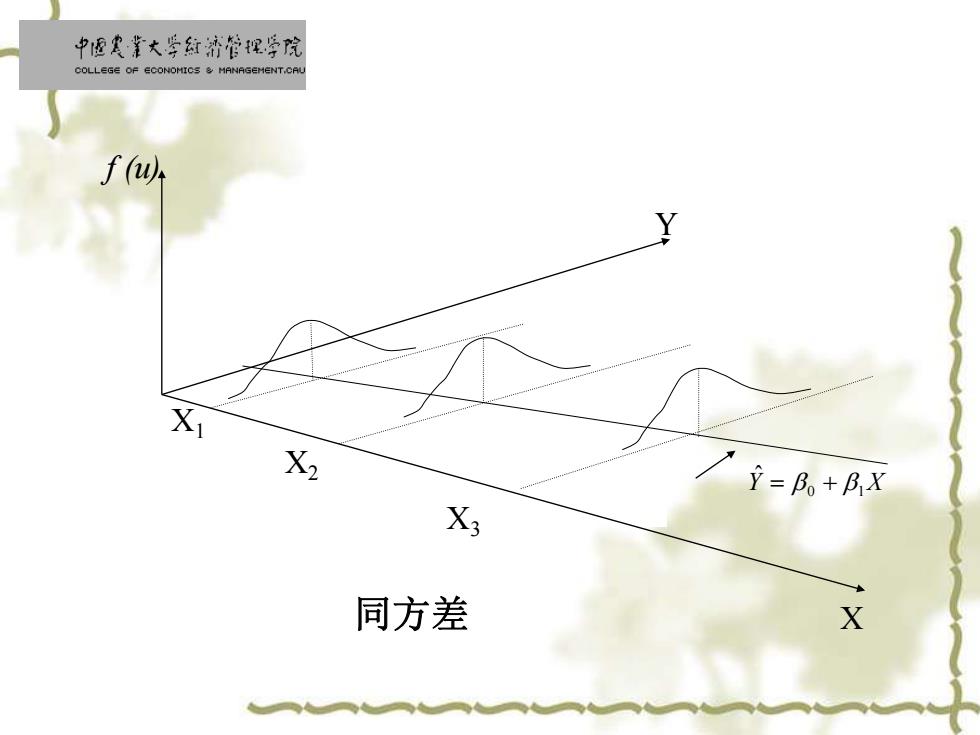
f (u) Y X3 X2 X1 X Y ˆ = 0 + 1 X 同方差

中面寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (三)一元线性回归模型参数最小二乘估 计量(O儿SE)的性质 一 元线性 Y=B。+BX+u 总体回归模型 回归模型 Y=bo+bX+e 样本回归模型 样本估计 1、估计量是线性的(Linear); 量的性质 2、估计量是无偏的 (Unbias)估计量(Estimator) E(bo)=Bo E(b)=B Var(bo) Var(b)=? 3、方差最小性(Best)Var(b)≤Var(b,) 4、b服从正态分布b~N(B,Var(b) b~N(Bar(b》
(三)一元线性回归模型参数最小二乘估 计量(OLSE)的性质 一元线性 回归模型 Y = 0 + 1 X +u Y = b +b X + e 0 1 总体回归模型 样本回归模型 样本估计 量的性质 1 、估计量是线性的(Linear); 2、估计量是无偏的(Unbias)估计量(Estimator) ( ) ? ( ) 0 0 0 = = Var b E b ( ) ? ( ) 1 1 1 = = Var b E b 3、方差最小性(Best) 4、b服从正态分布 ~ ( , ( )) ~ ( , ( )) 0 0 0 1 1 1 b N Var b b N Var b ( ) ( ) * Var bi Var bi

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 点估计的方法有多种。但最小二乘法(高斯-马尔 科夫定理)保证: 由最小二乘法得到的估计量是线性无偏的估计 量,而且是一个最好的估计量。即最小二乘估计量 (OLSE)具有BLUE性质。 BLUE:Best Linear Unbias Estimator
❖ 点估计的方法有多种。但最小二乘法(高斯-马尔 科夫定理)保证: 由最小二乘法得到的估计量是线性无偏的估计 量,而且是一个最好的估计量。即最小二乘估计量 (OLSE)具有BLUE性质。 ❖ BLUE:Best Linear Unbias Estimator
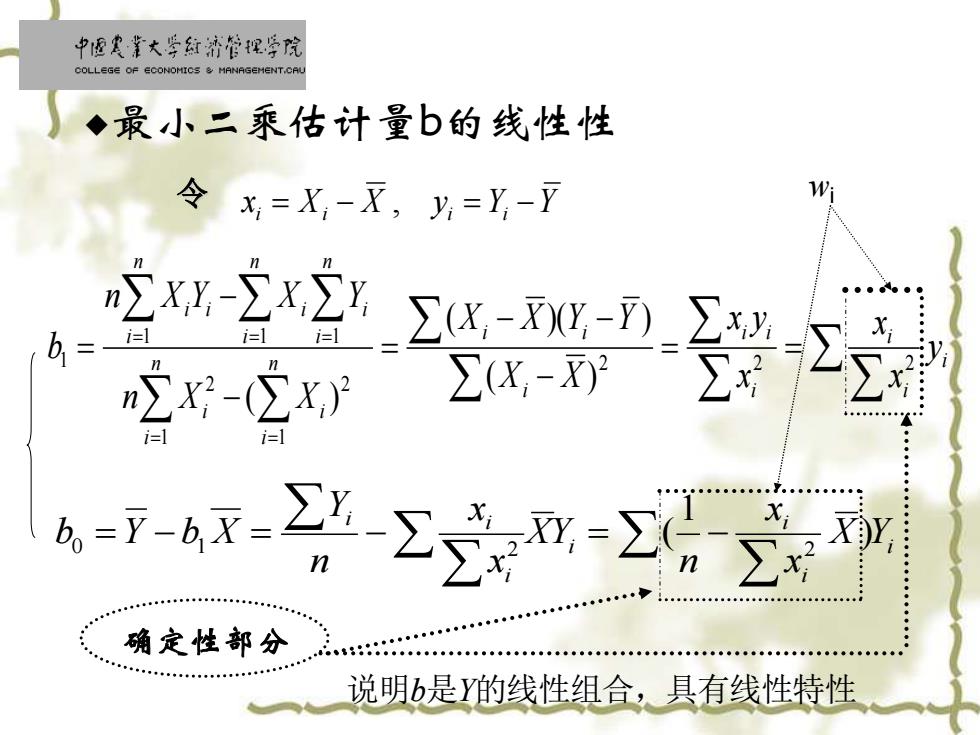
中面寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL ◆最小、二乘估计量b的线性性 令x=X-x,y=y-Y 正xw-2x2g- j=1 b= n∑x-(∑x,)2 ∑,-X∑x 6-4-2m2话 确定性部分 说明b是Y的线性组合,具有线性特性
= = − − − = − − = = = = = = i i i i i i i i i n i n i i i n i n i i i n i i i y x x x x y X X X X Y Y n X X n X Y X Y b 2 2 2 1 2 1 2 1 1 1 1 ( ) ( )( ) ( ) i i i i i i i X Y x x n XY x x n Y b Y b X = − = − = − ) 1 ( 0 1 2 2 ◆最小二乘估计量b的线性性 确定性部分 令 xi = Xi − X , yi = Yi −Y 说明b是Y的线性组合,具有线性特性 wi

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 令w= 则:b=∑w,Y b=∑(2-w,)y w的性质: ()∑w,=0 2)∑时=2买 (3)∑w,x,=1 (4)∑w,X,=1
i i i i w X Y n b b wY ) 1 ( 0 1 = − 则: = = 2 i i x x 令 w (4) 1 (3) 1 1 (2) (1) 0 2 2 = = = = i i i i i i i w X w x x w w 的性质: w