
用逆函数求上下分位点 ·将边界值Fb作为输入变元,可求得相应的分位点。: alpha=0.1; %取双边90%的置信区间 Fb=[alpha/2,1-alpha/2]%输入变元 ·%三种分布的双侧a分位点 lambda1=norminv(Fb,0,1) lambda2=chi2inv(Fb,10) lambda3=binoinv(Fb,10,0.2) 。 程序运行后得到 lambda1=-1.64491.6449 lambda:2=3.940318.3070 lambda3 0 4 这就是三种分布函数下的双边90%置信区间 。 改变alpha的值,可得到各种不同置信度下的置信区间
用逆函数求上下分位点 • 将边界值Fb作为输入变元,可求得相应的分位点。: alpha=0.1; % 取双边90%的置信区间 Fb =[alpha/2,1-alpha/2] % 输入变元 • % 三种分布的双侧α分位点 lambda1=norminv(Fb,0,1) lambda2=chi2inv(Fb,10) lambda3=binoinv(Fb,10,0.2) • 程序运行后得到 lambda1 = -1.6449 1.6449 lambda2 = 3.9403 18.3070 lambda3 = 0 4 这就是三种分布函数下的双边90%置信区间 • 改变alpha的值,可得到各种不同置信度下的置信区间

各种分布理论统计特性的计算 (Cc)_。对以上3种分布,MATLAB:还给出了它们的理论统计 参数,即理论均值Mu和方差值var的计算方法,所用的命 令为~stat。例如: [Mu1,var1]=normstat(0,1) [Mu2,var2]=chi2stat(10) [Mu3,var3]=binostat(10,.2) ·运行结果为: ·Mu1=0,var1=1 ·Mu2=10,Var2=20 ·Mu3=2,var3=1.6000 本题虽然只给出了3种分布的计算,这些概念和方法可以 类推到表5-6-1中20种分布的理论计算中
各种分布理论统计特性的计算 • (c) 。对以上3种分布,MATLAB还给出了它们的理论统计 参数,即理论均值Mu和方差值var的计算方法,所用的命 令为~stat。例如: • [Mu1,var1]= normstat(0,1) • [Mu2,var2]= chi2stat(10) • [Mu3,var3]= binostat(10,.2) • 运行结果为: • Mu1 = 0, var1 = 1 • Mu2 = 10,var2 = 20 • Mu3 = 2,var3 = 1.6000 • 本题虽然只给出了3种分布的计算,这些概念和方法可以 类推到表5-6-1中20种分布的理论计算中
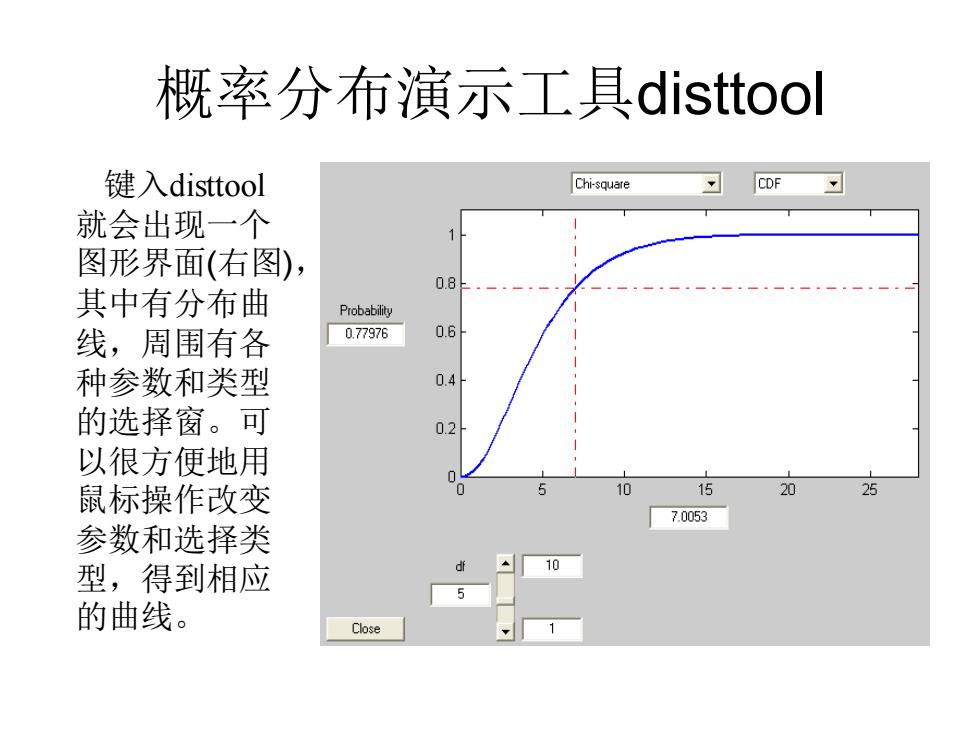
概率分布演示工具disttool 键入disttool Chi-square CDF✉ 就会出现一个 图形界面(右图), 08 其中有分布曲 Probability 线,周围有各 0.77976 0.6 种参数和类型 04 的选择窗。可 0.2 以很方便地用 鼠标操作改变 15 7.0053 参数和选择类 型,得到相应 410 5 的曲线。 Close 1
概率分布演示工具disttool 键入disttool 就会出现一个 图形界面(右图), 其中有分布曲 线,周围有各 种参数和类型 的选择窗。可 以很方便地用 鼠标操作改变 参数和选择类 型,得到相应 的曲线