
5.2节 解析几何和多变量函数
5.2节 解析几何和多变量函数

5.2节 解析几何和多变量分析 0 本节主要讨论用MATLAB解决空间解析几何 的问题。重点是利用MATLAB的三维作图功 能,对多变量函数的性质进行更为形象的 讨论。 ·读者要从中学会曲面的绘制方法,等高线 图和方向导数(梯度)的计算和绘制,进 一步把它们的几何意义与解析表示式联系 起来
5.2节 解析几何和多变量分析 • 本节主要讨论用MATLAB解决空间解析几何 的问题。重点是利用MATLAB的三维作图功 能,对多变量函数的性质进行更为形象的 讨论。 • 读者要从中学会曲面的绘制方法,等高线 图和方向导数(梯度)的计算和绘制,进 一步把它们的几何意义与解析表示式联系 起来

极坐标系中的绘图 【例5-2-1】绘制极坐标系下的平面曲线 p=acos(b+ne) 并讨论参数a、b、n的影响。 ·◆建模绘图的基本方法仍然是先设置自变量数 组,按元数群运算的要求列出函数表示式,使得 一个表示式能够同时计算出与自变量数目相等的 因变量,立即可用来绘图。为了便于比较,编一 个能分别画出两个图形的程序,采用fo循环,读 者可从中看到利用循环指数的技巧。 ·由于有两种参数下的数据,因变量也有两组数据, 所以ho要设成二维的数组
极坐标系中的绘图 【例5-2-1】 绘制极坐标系下的平面曲线 并讨论参数a、b、n的影响。 • ◆建模 绘图的基本方法仍然是先设置自变量数 组,按元数群运算的要求列出函数表示式,使得 一个表示式能够同时计算出与自变量数目相等的 因变量,立即可用来绘图。为了便于比较,编一 个能分别画出两个图形的程序,采用for循环,读 者可从中看到利用循环指数的技巧。 • 由于有两种参数下的数据,因变量也有两组数据, 所以rho要设成二维的数组。 = + a b n cos( )

极坐标绘图程序exn521 theta=0:0.1:2*pi;%产生自变量(极角)向量 %或用theta=:linspace(0,2*pi,N); for i=1:2 a(0=input('a=(书上值为a(1)=2;a(2)=2); b(0=input('b=(书上值为b(1)=pil4;b(2)=0)): n(0=input('n=(书上值为n(1)=2;n(2)=3) rho(i,:)=a()*cos(b()+n()*theta);%因变量方程 subplot(1,2,i),polar(theta,rho(i,:);%绘图 end
极坐标绘图程序exn521 theta=0:0.1:2*pi; % 产生自变量(极角)向量 % 或用 theta=linspace(0,2*pi,N); for i=1:2 a(i)=input('a= (书上值为a(1)=2;a(2)=2)'); b(i)=input('b= (书上值为b(1)=pi/4;b(2)=0)'); n(i)=input('n= (书上值为n(1)=2;n(2)=3)') rho(i,:)=a(i)*cos(b(i)+n(i)*theta); %因变量方程 subplot(1,2,i),polar(theta,rho(i,:)); %绘图 end
极坐标绘图程序的输出图形 ◆运行并输入不同参数的结果如图5-1-2。 a=2;b=pi/4;n=2 (四叶玫瑰线) a=2;b=0;n=3 (三叶玫瑰线) 1209 1.9981 .99904 150 150 18 18 21仅 330 21 30 240270300 24027000
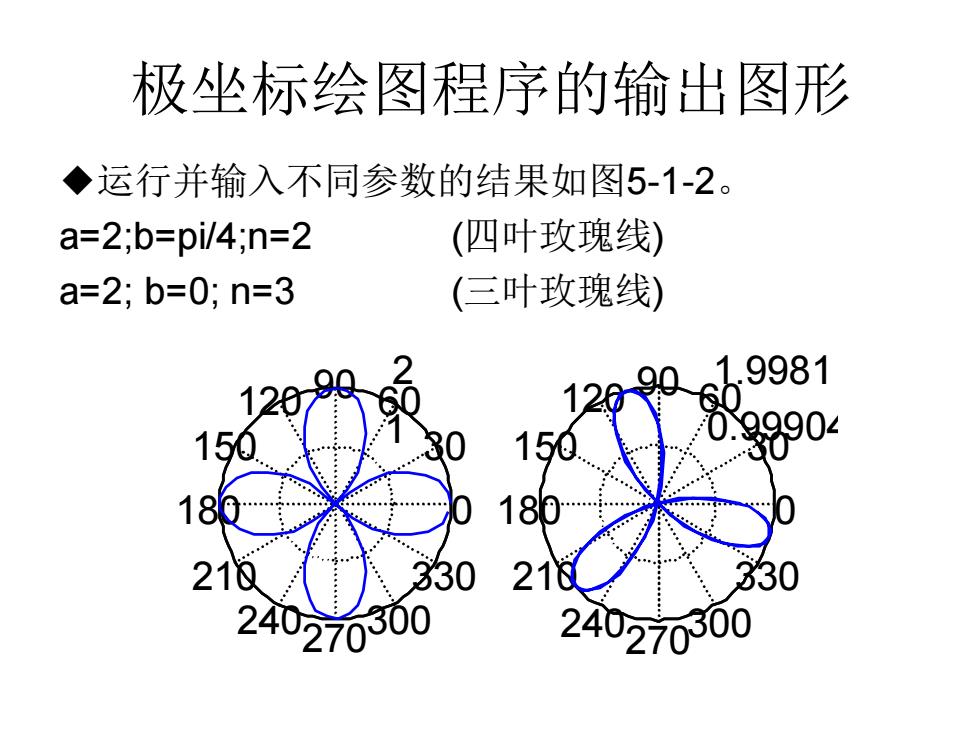
极坐标绘图程序的输出图形 ◆运行并输入不同参数的结果如图5-1-2。 a=2;b=pi/4;n=2 (四叶玫瑰线) a=2; b=0; n=3 (三叶玫瑰线) 1 2 30 210 60 240 90 270 120 300 150 330 180 0 0.99904 1.9981 30 210 60 240 90 270 120 300 150 330 180 0