西安电子科技大学：《MATLAB及其在电子信息课程中的应用》课程PPT教学课件（讲稿）第六章 在信号与系统中的应用

第6章在信号与系统中的应用

第 6章 在信号与系统中的应用

例6.1连续信号的MATLAB描述 (1)单位冲激函数 1/A x0=8-0F0 t<t<t,+△ 其余 (2)单位阶跃函数： x,0=-h)=0 1 1<t<t1+△ t<0 (3)复指数函数 x3(t)=e(u+jo)t

例6.1 连续信号的MATLAB描述 （1）单位冲激函数 （2）单位阶跃函数： （3）复指数函数 1 1 1 1 1 ( ) ( ) 0 t t t x t t t       +  = − =   其余       +  = − = 0 0 1 ( ) ( ) 1 1 2 1 t t t t x t u t t u t x t ( j ) ( ) e 3 +  =

例6.2LTI系统的零输入响应 ·n阶线性时不变连续系统的微分方程 d"y d"-ly 4dr+a dt a盘+=+ 己知y及其各阶导数的初始值为y(O),y)(O),., yn)(O),求系统的零输入响应。 ·解：方程的解为 y(t)=Cie+Ce+..+Cep p1,p2…,Pn是方程a12+a22n-1+..+an+ant1=0的根， C1,,Cn由y及其各阶导数的初始值来确定

例6.2 LTI系统的零输入响应 • n阶线性时不变连续系统的微分方程 已知y及其各阶导数的初始值为y(0),y (1)(0)，…， y (n-1)(0)，求系统的零输入响应。 • 解：方程的解为 p1 , p2…,pn是方程a1 n+a2 n-1+…+ an+ an+1 =0的根, C1，…，Cn由y及其各阶导数的初始值来确定。 , d d d d d d d d d d 1 1 1 1 1 2 b u t u b t u a y b t y a t y a t y a m m m m n n n n n + + − + ++ + = ++ + p t n p t p t C C C n y(t) e e e 1 2 = 1 + 2 ++

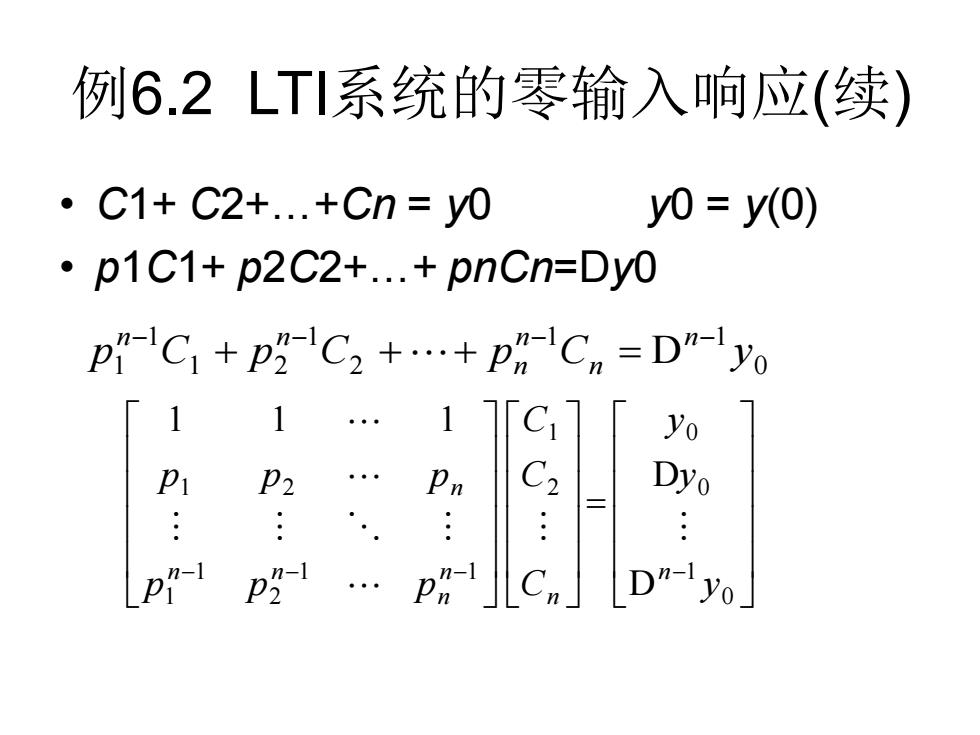
例6.2LT系统的零输入响应（续） 。C1+C2+..+Cn=y0 yo=y(0) .p1C1+p2C2+...+pnCn=Dy0 p"C+p2-C2++pCn D"yo 1 Dyo pa-1

例6.2 LTI系统的零输入响应(续) • C1+ C2+…+Cn = y0 y0 = y(0) • p1C1+ p2C2+…+ pnCn=Dy0 0 1 1 2 1 1 2 1 p1 C p C p C D y n n n n n− n− − − + ++ =             =                         − − − − 0 1 0 0 2 1 1 1 2 1 1 1 2 D D 1 1 1 y y y C C C p p p p p p n n n n n n n         

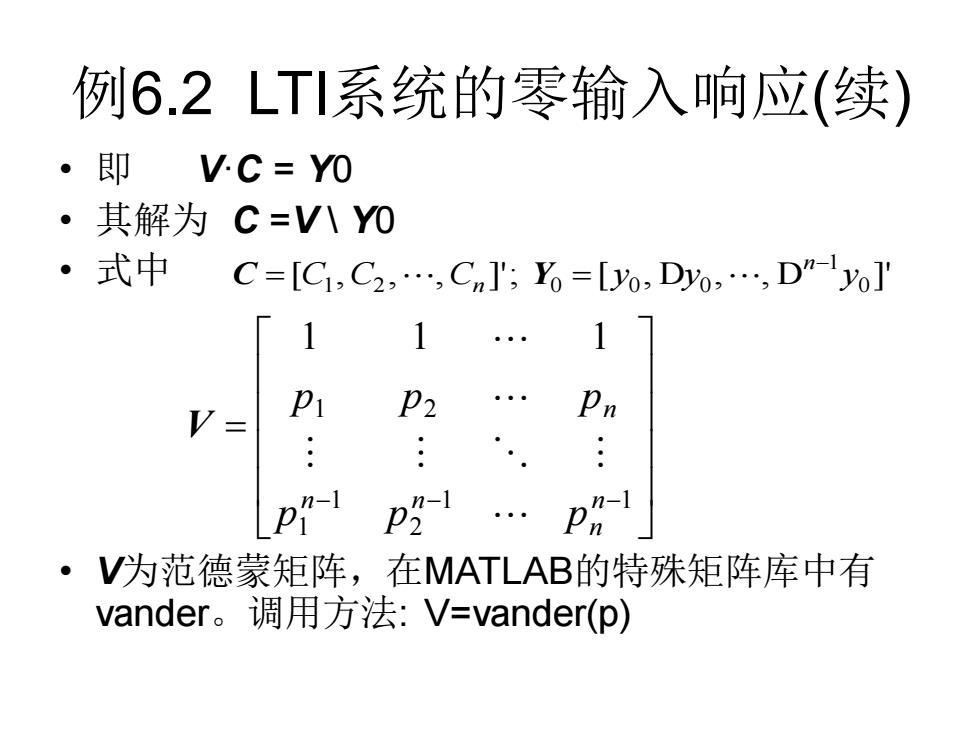
例6.2LTI系统的零输入响应（续） 。即VC=YO ·其解为C=V八Y0 ·式中 C=[C1,C2,…,Cn]';=[0,Dyo,…,D”yo] 1 1 V= P2 Pn p- P- ·V为范德蒙矩阵，在MATLAB的特殊矩阵库中有 vander。.调用方法：V=vander(p)

例6.2 LTI系统的零输入响应(续) • 即 V·C = Y0 • 其解为 C =V \ Y0 • 式中 • V为范德蒙矩阵，在MATLAB的特殊矩阵库中有 vander。调用方法: V=vander(p) [ , , , ]'; [ , D , , D ]' 0 1 1 2 0 0 0 C C C y y y n n − C =  Y =              = − −1 −1 2 1 1 1 2 1 1 1 n n n n n p p p p p p        V