
5.6节概率论与数理统计
5.6节 概率论与数理统计

各种统计分布函数 0 表5-6-1中列出了20种分布函数,统计工具 箱提供了包括分布函数~cdf(Cumulattive Distribution Function)、概率密度函数 ~pdf(Probability Distribution Function)、分 布函数的逆函数~inv(Inverse Cumulattive Distribution Function)以及这些分布的理论 统计特性(均值和方差)计算函数~stat
一 各种统计分布函数 • 表5-6-1中列出了20种分布函数,统计工具 箱提供了包括分布函数~cdf(Cumulattive Distribution Function)、概率密度函数 ~pdf(Probability Distribution Function)、分 布函数的逆函数~inv(Inverse Cumulattive Distribution Function) 以及这些分布的理论 统计特性(均值和方差)计算函数~stat
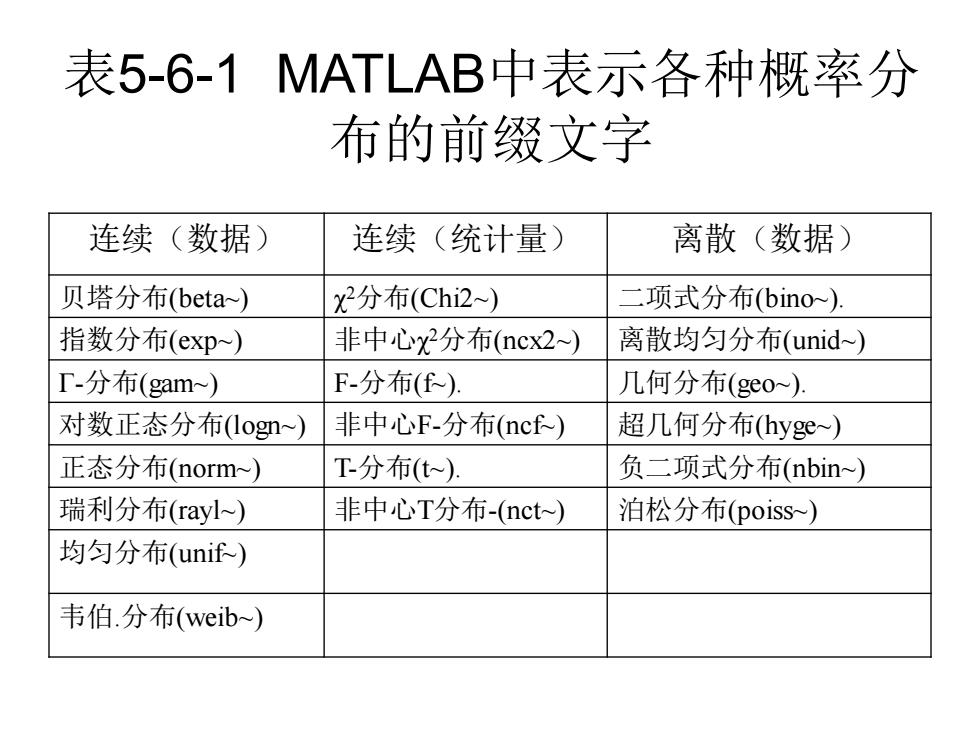
表5-6-1 MATLAB中表示各种概率分 布的前缀文字 连续(数据) 连续(统计量) 离散(数据) 贝塔分布(beta-) x2分布(Chi2~)》 二项式分布(bino~). 指数分布(exp~) 非中心x分布ncx2~) 离散均匀分布(unid~) T-分布(gam) F-分布(). 几何分布(geo~). 对数正态分布(logn~) 非中心F-分布(ncf~) 超几何分布(hyge~) 正态分布(norm) 工分布(t) 负二项式分布(nbin~) 瑞利分布(rayl~) 非中心T分布-(nct) 泊松分布(poiss) 均匀分布(unif) 韦伯.分布(weib~)
表5-6-1 MATLAB中表示各种概率分 布的前缀文字 连续(数据) 连续(统计量) 离散(数据) 贝塔分布(beta~) χ 2分布(Chi2~) 二项式分布(bino~). 指数分布(exp~) 非中心χ 2分布(ncx2~) 离散均匀分布(unid~) Г-分布(gam~) F-分布(f~). 几何分布(geo~). 对数正态分布(logn~) 非中心F-分布(ncf~) 超几何分布(hyge~) 正态分布(norm~) T-分布(t~). 负二项式分布(nbin~) 瑞利分布(rayl~) 非中心T分布-(nct~) 泊松分布(poiss~) 均匀分布(unif~) 韦伯.分布(weib~)

表5-6-1的使用方法 把表中不同分布后面括号中的文字作为前缀,把 所需计算的特性作为后缀,就可以组合成一个函 数。例如离散类的二项式分布有binopdf,binocdf, binoinv,.binostat四个函数,连续类数据的标准正 态分布有normpdf,normcdf,,norminv,normstat四 个函数,连续类统计量的X2分布有chi2pdf, chi2cdf,chi2inv,chi2stat四个函数,.等等,20 种分布就有80个函数。由于各种分布函数的解析 形式都是已知的,这些子程序的编写并不困难
表5-6-1的使用方法 • 把表中不同分布后面括号中的文字作为前缀,把 所需计算的特性作为后缀,就可以组合成一个函 数。例如离散类的二项式分布有binopdf, binocdf, binoinv, binostat四个函数,连续类数据的标准正 态分布有normpdf, normcdf, norminv, normstat四 个函数,连续类统计量的χ2分布有chi2pdf, chi2cdf, chi2inv, chi2stat四个函数,…等等,20 种分布就有80个函数。由于各种分布函数的解析 形式都是已知的,这些子程序的编写并不困难

【例5-6-1】概率分布曲线的绘制 【例5-6-1】(a)求标准正态分布N(0,1),自由度V=10的X2 分布和N=10,p=0.2的二项式分布B(10,0.2)的分布函数, 并画出其概率密度曲线和分布曲线;(b)。求出分布函数 为0.05和0.95处的随机变量值;(c).。求出这几个分布的 均值和方差。 解:分别键入help normpdf,.help binopdf,help chi2pdf以 了解它们的用法,特别是了解输入变元的意义,得知: f=normpdf(x,mu,sigma) 其中x为随机变量数组,mu为均值,sigma为标准差。 f=chi2pdf(x,V) 其中x为随机变量数组,V为自由度数(整数), f=binopdf(x,N,p) 其中x为随机变量整数数组,N为次数,0≤P≤1为成功概率
【例5-6-1】概率分布曲线的绘制 • 【例5-6-1】(a)求标准正态分布N(0,1),自由度V=10的χ 2 分布和N=10,p=0.2的二项式分布B(10,0.2)的分布函数, 并画出其概率密度曲线和分布曲线;(b) 。求出分布函数 为0.05和0.95处的随机变量值;(c) 。求出这几个分布的 均值和方差。 • 解:分别键入help normpdf, help binopdf, help chi2pdf 以 了解它们的用法,特别是了解输入变元的意义,得知: f=normpdf(x,mu,sigma) 其中x为随机变量数组,mu为均值,sigma为标准差。 f=chi2pdf(x,V) 其中x为随机变量数组,V为自由度数(整数), f=binopdf(x,N,p) 其中x为随机变量整数数组,N为次数,0≤p≤1为成功概率