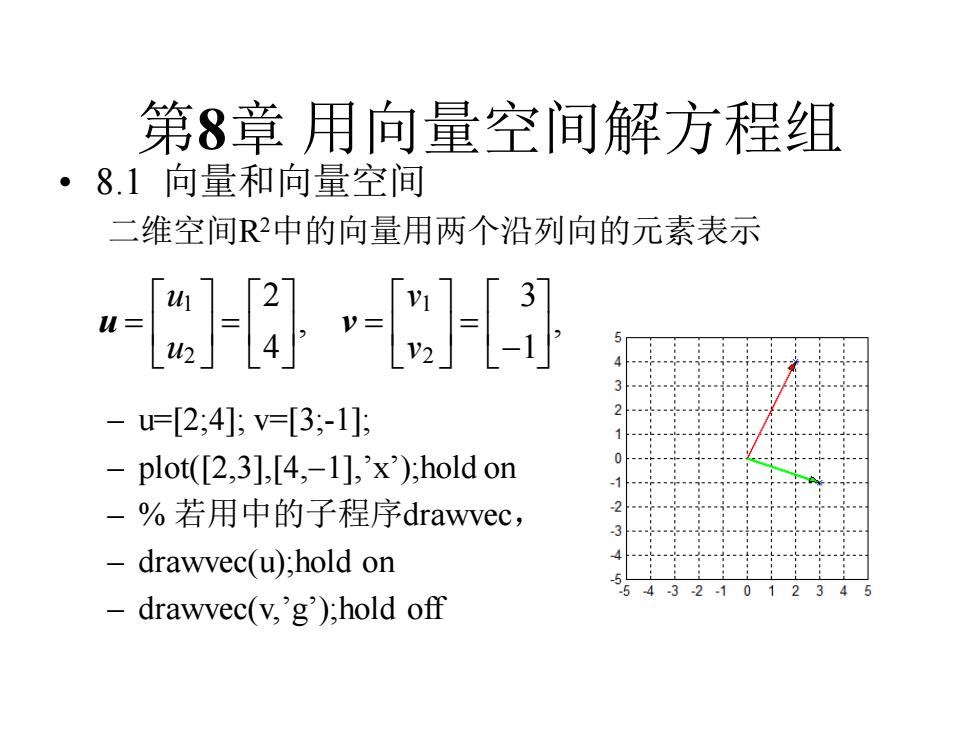
第8章用向量空间解方程组 ·8.1向量和向量空间 二维空间R2中的向量用两个沿列向的元素表示 u= -u=[2;4];V=[3;1]; 2 -plot([2,3],[4,-1],'x);hold on 0 -%若用中的子程序drawvec, 2 drawvec(u);hold on 5-4-3-21012345 drawvec(v,'g');hold off
第8章 用向量空间解方程组 • 8.1 向量和向量空间 二维空间R2中的向量用两个沿列向的元素表示 – u=[2;4]; v=[3;-1]; – plot([2,3],[4,−1],’x’);hold on – % 若用中的子程序drawvec, – drawvec(u);hold on – drawvec(v,’g’);hold off 1 1 2 2 2 3 , , 4 1 u v u v = = = = − u v

二维向量张成的空间 平面上的任何一点[w1w2]是不是一定能用u和v的线性 组合来实现?即是不是一定能找到一组常数[C1,c2],使 得 f[[l c,C2取所有可能的值,得到的w的集合就是u和v张成的 子空间,在所给的u和v下,它是一个平面。 0 若和v两个向量的各元素成简单的比例关系,合成的 向量只能在一根直线上,不可能张成整个二维平面。 这种情况下,称这两个向量和v是线性相关的
二维向量张成的空间 • 平面上的任何一点[w1 ;w2 ]是不是一定能用u和v的线性 组合来实现?即是不是一定能找到一组常数[c1 ,c2 ],使 得 • c1 ,c2取所有可能的值,得到的w的集合就是u和v张成的 子空间,在所给的u和v下,它是一个平面。 • 若u和v两个向量的各元素成简单的比例关系,合成的 向量只能在一根直线上,不可能张成整个二维平面。 这种情况下,称这两个向量u和v是线性相关的。 1 1 2 2 2 3 4 1 w c c w + = −

2.三维空间中的向量 。1 若yy,和y都是三维空间的列向量。可以用空间坐 标中的三个点,或从坐标原点引向这三点的箭头 来表示。用矩阵代数表示如下 -3 1 -7 0 ·如果三个基本向量之间线性无关,那么它们的线 性组合可以覆盖(张成)整个三维空间。如果三 个向量共面,即相关,就不能张成三维空间。判 断三个向量的线性相关性,可用行列式
2.三维空间中的向量 • 若v1 ,v2和v3都是三维空间的列向量。可以用空间坐 标中的三个点,或从坐标原点引向这三点的箭头 来表示。用矩阵代数表示如下 • 如果三个基本向量之间线性无关,那么它们的线 性组合可以覆盖(张成)整个三维空间。如果三 个向量共面,即相关,就不能张成三维空间。判 断三个向量的线性相关性,可用行列式。 1 5 3 1 , 4 , 1 , 2 7 0 − = − = − = − − v v v 1 2 3

三维空间向量的相关性 ·即看三向量并列所得矩阵的行列式 15-3 A=[,2,3]=-1-41g -2-70 ·det(A)=0相关 ● det(A)0不相关 行列式的几何意义:在二维是两个向量组成的平 行四边形面积,在三维是三个向量组成的平行 六面体的体积
三维空间向量的相关性 • 即看三向量并列所得矩阵的行列式 • det(A)=0 相关 • det(A)≠0 不相关 • 行列式的几何意义:在二维是两个向量组成的平 行四边形面积,在三维是三个向量组成的平行 六面体的体积。 153 1 4 1 , 2 7 0 − = = − − − − A v ,v ,v 1 2 3
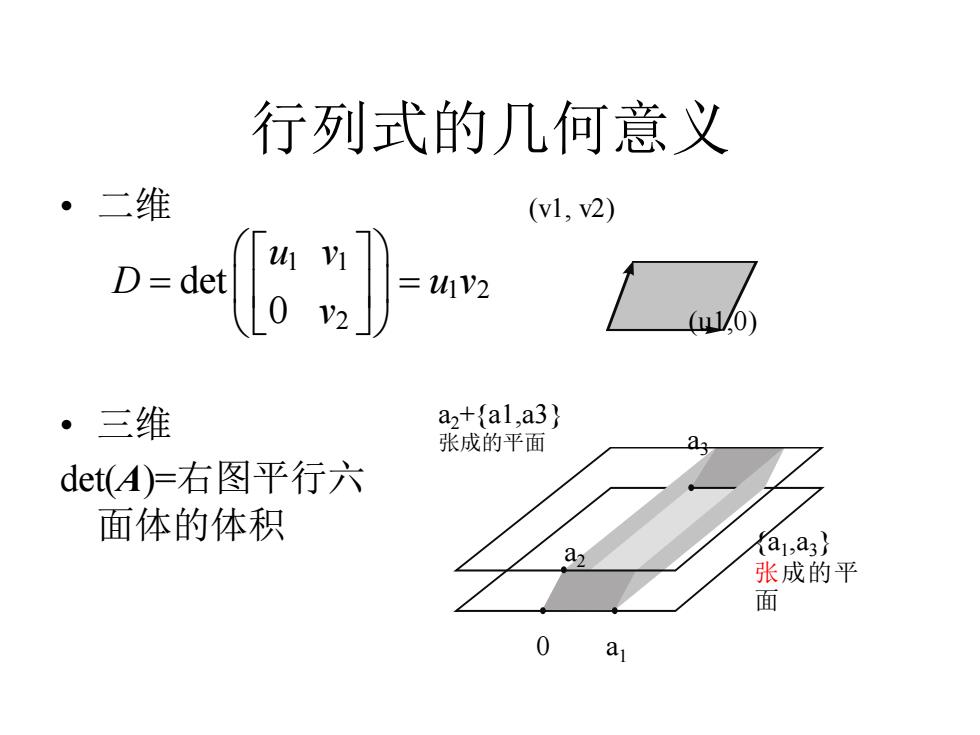
行列式的几何意义 二维 (1,v2) ujv2 0) ·三维 a2+{al,a3} 张成的平面 det(A)=右图平行六 面体的体积 a1,a3} 张成的平 0 a
行列式的几何意义 • 二维 • 三维 det(A)=右图平行六 面体的体积 (v1, v2) (u1,0) a2+a1,a3 张成的平面 a1 ,a3 张成的平 面 a3 a2 0 a1 1 1 1 2 2 det 0 u v D u v v = =