《概率论与数理统计》课程教学课件（PPT讲稿）第08章 假设检验 8.3 正态总体方差的假设检验

概率论与数理统外「 2 2 001 J(n-1)S2 (因为o2≤o,2) 要使P{H,为真拒绝H}≤a, 只满令p:。-a 因为0s-xm-1所以axm-l 00

           ( 1) ( 1) 2 0 2 0 2 2 0 2     n S n k P ( ) ( 1) ( 1) 2 0 2 2 0 2 2 2 0 2                   因 为 n S n k P { } , 要使 P H0 为真拒绝H0  . ( 1) ( 1) 2 0 2 2 2 0 2                 n S n k 只需令 P ~ ( 1), ( 1) 2 2 2   n n S   因为 ~ ( 1), ( 1) 2 2 0   n n k    所以

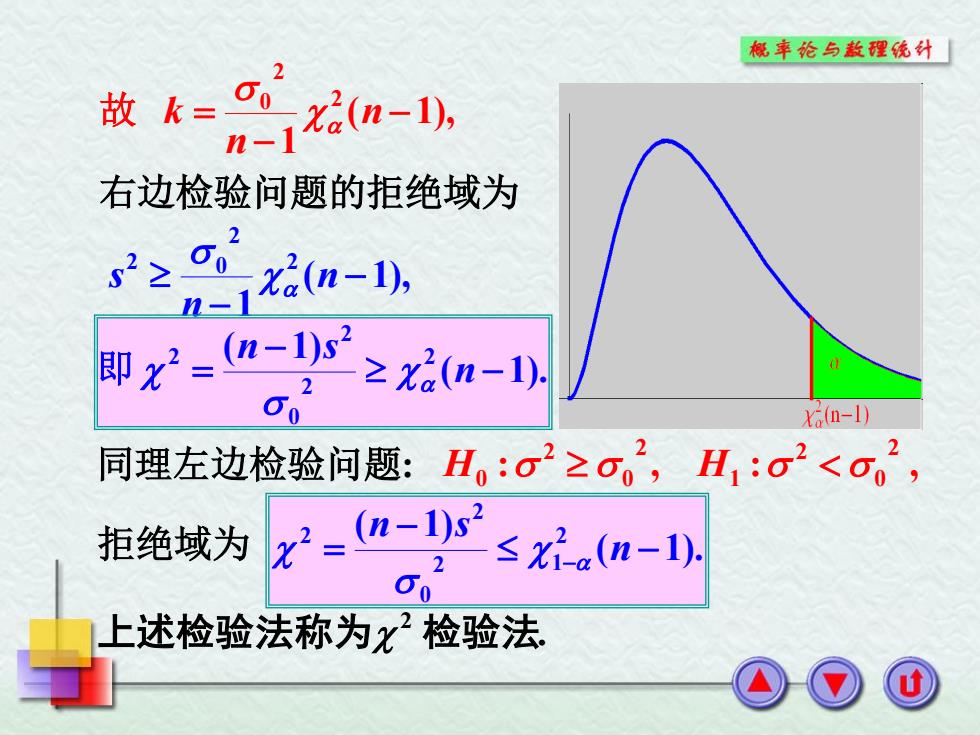
概率论与敖理统外 2 n1n-, 故k= 右边检验问题的拒绝域为 0 52≥ x2(n-1), 即-a2z- Xa(n-1) 同理左边检验问题：H,:σ2之o, 2 H1:σ2<o0, 拒绝域为 z2=" ≤a(n-1). 上述检验法称为x检验法

( 1), 1 2 2 0    n n k    故 ( 1), 1 2 2 2 0    n n s    右边检验问题的拒绝域为 ( 1). ( 1) 2 2 0 2 2     n n s    即 同理左边检验问题: : , : , 2 0 2 1 2 0 2 H0   H   拒绝域为 ( 1). ( 1) 2 2 1 0 2 2      n n s     . 上述检验法称为 2 检验法