
第二节 离散型随机变量 及其分布律 一、离散型随机变量的分布律 二、常见离散型随机变量的概率分布
一、离散型随机变量的分布律 二、常见离散型随机变量的概率分布 第二节 离散型随机变量 及其分布律

一、离散型随机变量的分布律 定义 设离散型随机变量X所有可能取的值为 xk(k=1,2,.),X取各个可能值的概率,即事件 {X=X}的概率为 P{X=X}=pk,k=1,2,. 称此为离散型随机变量X的分布律. 说明 (1)pk≥0,k=1,2,; (2)∑:=1. k=
说明 (1) p 0, k = 1,2, ; k (2) 1. 1 = k= pk . { } , 1,2, . { } , ( 1,2, ), , 称此为离散型随机变量 的分布律 的概率 为 取各个可能值的概率 即事件 设离散型随机变量 所有可能取的值为 X P X x p k X x x k X X k k k k = = = = = 一、离散型随机变量的分布律 定义
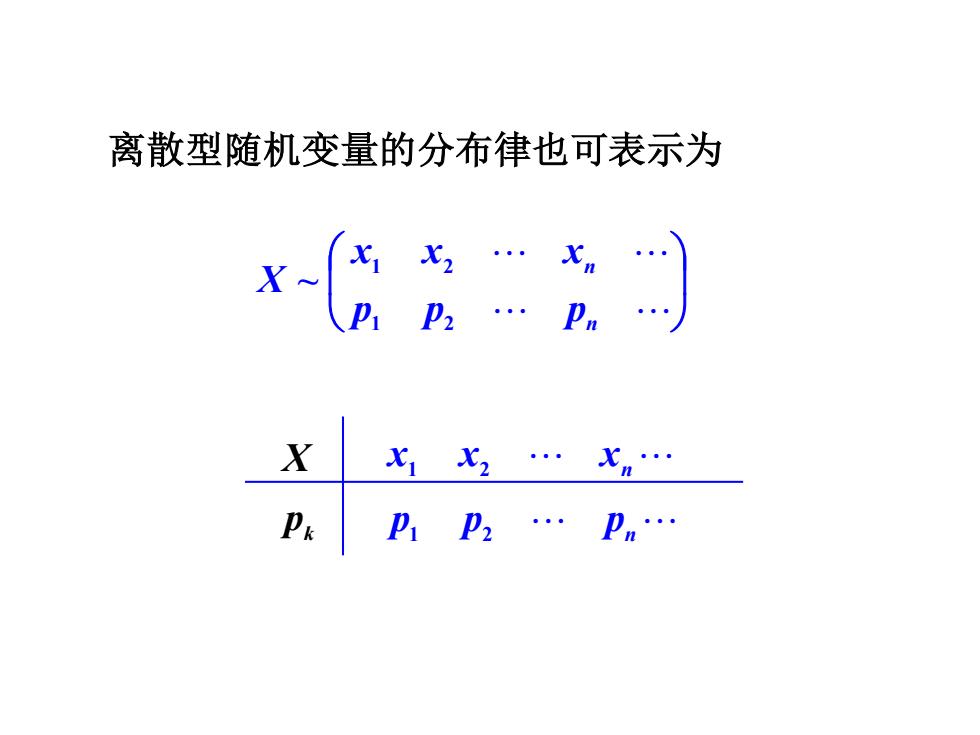
离散型随机变量的分布律也可表示为
离散型随机变量的分布律也可表示为 n n p p p x x x X 1 2 1 2 ~ X pk x1 x2 xn p1 p2 pn

例1设一汽车在开往目的地的道路上需经过四 组信号灯,每组信号灯以1/2的概率允许或禁止汽 车通过以X表示汽车首次停下时,它已通过的信 号灯的组数(设各组信号灯的工作是相互独立的), 求X的分布律. 解 X 2 P 0.5 0.25 0.125 0.0625 0.0625
. ( ), . , , 1 2 求 的分布律 号灯的组数 设各组信号灯的工作是相互独立的 车通过 以 表示汽车首次停下时 它已通过的信 组信号灯 每组信号灯以 的概率允许或禁止汽 设一汽车在开往目的地的道路上需经过四 X X 解例 1 Xk p 0 1 2 3 4 0.5 0.25 0.125 0.0625 0.0625

二、常见离散型随机变量的概率分布 1.两点分布 设随机变量X只可能取0与1两个值,它的分 布律为 0 则称X服从0一1)分布或两点分布:
二、常见离散型随机变量的概率分布 设随机变量 X 只可能取0与1两个值 , 它的分 布律为 X k p 0 1− p 1 p 则称 X 服从 (0—1) 分布或两点分布. 1.两点分布