《概率论与数理统计》课程教学资源（PPT课件）第2章 随机变量及其分布 第四节 连续型随机变量及其概率密度

概率伦与款理统外 第四节 连续型随机变量及其概率密度 一、概率密度的概念与性质 二、常见连续型随机变量的分布

一、概率密度的概念与性质 二、常见连续型随机变量的分布 第四节 连续型随机变量及其概率密度

概车纶与款理统外 一、概率密度的概念与性质 1.定义对于随机变量X的分布函数F(x), 如果存在非负函数(x),对于任意实数x有 F(x)=f(dt, 则称X为连续型随机变量，函数f(x), 称为X的概率密度函数，简称概率密度

一、概率密度的概念与性质 ( ) ( )d , x F x f t t − =  X f x( ), 1.定义 对于随机变量 的分布函数 如果存在非负函数 F x( ), 对于任意实数 x 有 则称 X 为连续型随机变量，函数 f x( ), 称为 X 的概率密度函数，简称概率密度

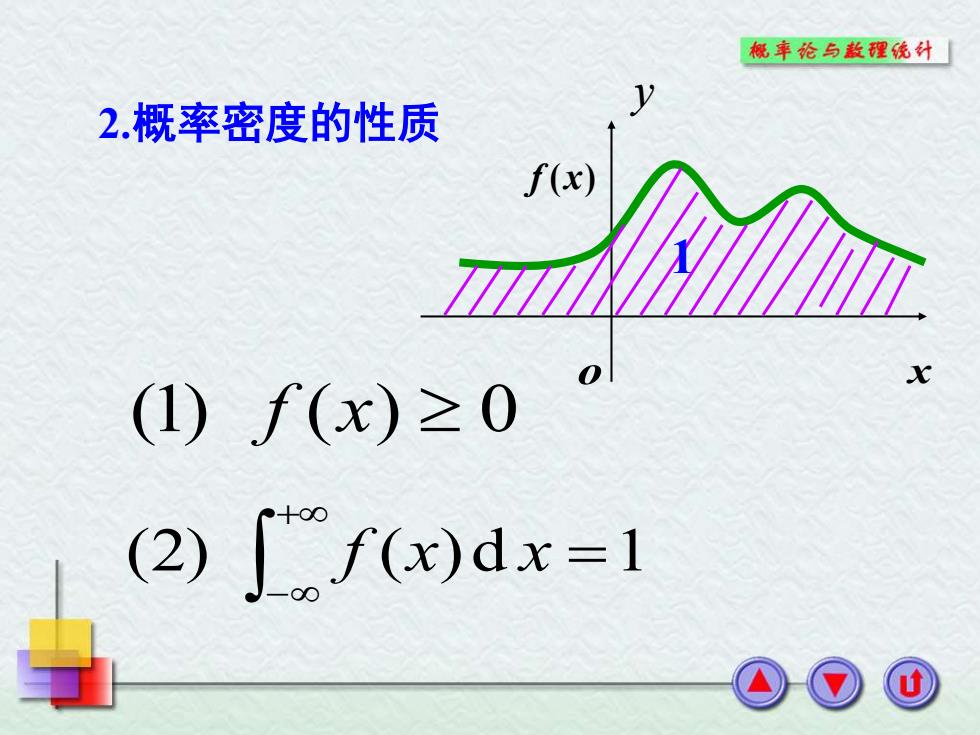
概華论与款程统外 2.概率密度的性质 f(x) 1)f(x)≥0 (2)f(x)dx=1

2.概率密度的性质 o x f (x) 1 (1) f (x)  0 (2) ( )d =1  + − f x x y

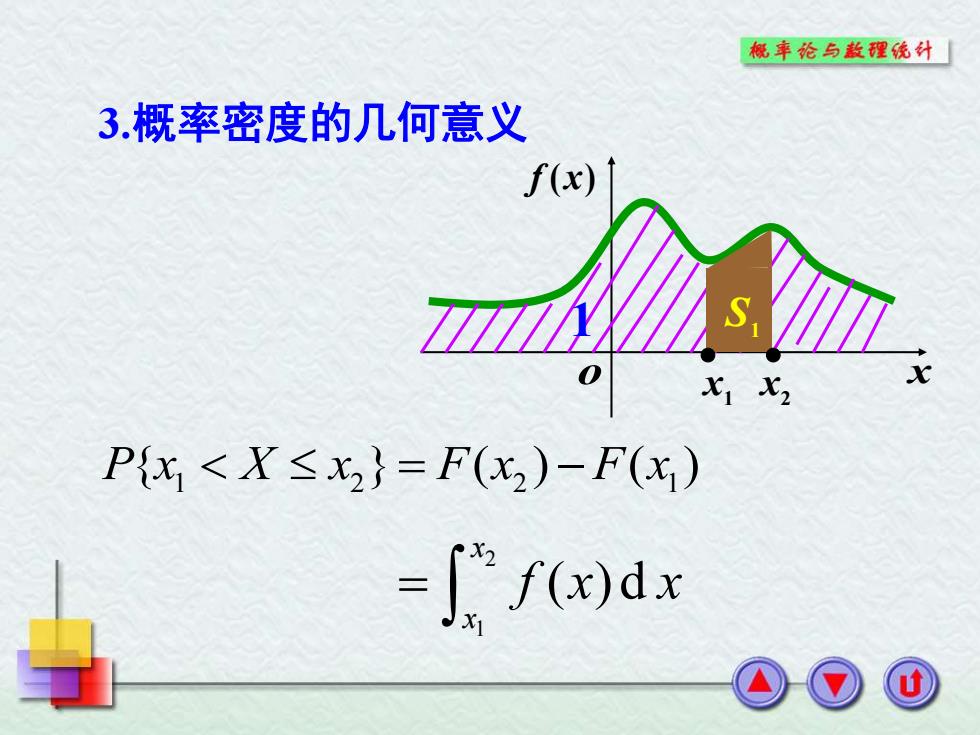
棍丰伦与散理统针」 3.概率密度的几何意义 f(x) X X2 Px<X<x)=F(x2)-F(x) -Jf()dx

o x f (x) 1 S1 1 x • 2 x • 3.概率密度的几何意义 1 2 2 1 P x X x F x F x { } ( ) ( )   = − 2 1 ( )d x x = f x x 

概華论与款醒硫外 注1 (I)P{X≤=Fa)=”f(x)dx, (2)P{X>=1-P{X≤=1-F(a) =f(x)dx. (3)在x)的连续点处F'(x)=∫(x)

P{X  a} = F(a) f (x)d x, a − = P{X  a} = 1 − P{X  a}= 1− F(a) f (x)d x. a  = 注1 （1） （2） （3）在 f(x) 的连续点处 F x f x ( ) ( ) =