
线性代数敖程 第三章矩阵的初等变换与线性方程组 23:45 小结R(A)=R(B)=n台Ax=b有唯一解 R(A)=R(B)<n台Ar=b有无穷多解 定义:含有个参数的方程组的任一解,称为线性 方程组的通解。 齐次线性方程组:系数矩阵化成行最简形矩阵, 便可写出其通解, 非齐次线性方程组:增广矩阵化成行阶梯形矩 阵,便可判断其是否有解.若有解,化成行最 简形矩阵,便可写出其通解, 第6顾
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第6页 小结 R(A)= R(B)= n Ax = b有唯一解 R(A)= R(B) n Ax = b有无穷多解. 方程组的通解. 定义:含有个参数的方程组的任一解,称为线性 齐次线性方程组:系数矩阵化成行最简形矩阵, 便可写出其通解; 非齐次线性方程组:增广矩阵化成行阶梯形矩 阵,便可判断其是否有解.若有解,化成行最 简形矩阵,便可写出其通解;

线性代数赦程第三章矩阵的初等变换与线性方程组 2345 二、线性方程组的解法 例1求解齐次线性方程组 x1+2x2+x3+x4=0 2x1+x2-2x3-2x4=0 x1-x2-4x3-3x4=0 解对系数矩阵A施行初等行变换: 5-2 0221 A= 0-3-6-4 1-1-4-3 0-3-6-4 第7页
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第7页 例1 求解齐次线性方程组 . 4 3 0 2 2 2 0 2 0 1 2 3 4 1 2 3 4 1 2 3 4 - - - = + - - = + + + = x x x x x x x x x x x x 解 - - - = - - 1 1 4 3 2 1 2 2 1 2 2 1 A - - - - - - 0 3 6 4 0 3 6 4 1 2 2 1 二、线性方程组的解法 对系数矩阵 A施行初等行变换: 3 1 2 2 1 r r r r - -
线性代数敖程 第三章矩阵的初等变换与线性方程组 23:45 10-2 5-3 5-h 2÷3) E 012 5-2 012 0 即得与原方程组同解的方程组 5-4% 4 +2x+3=0 第8项
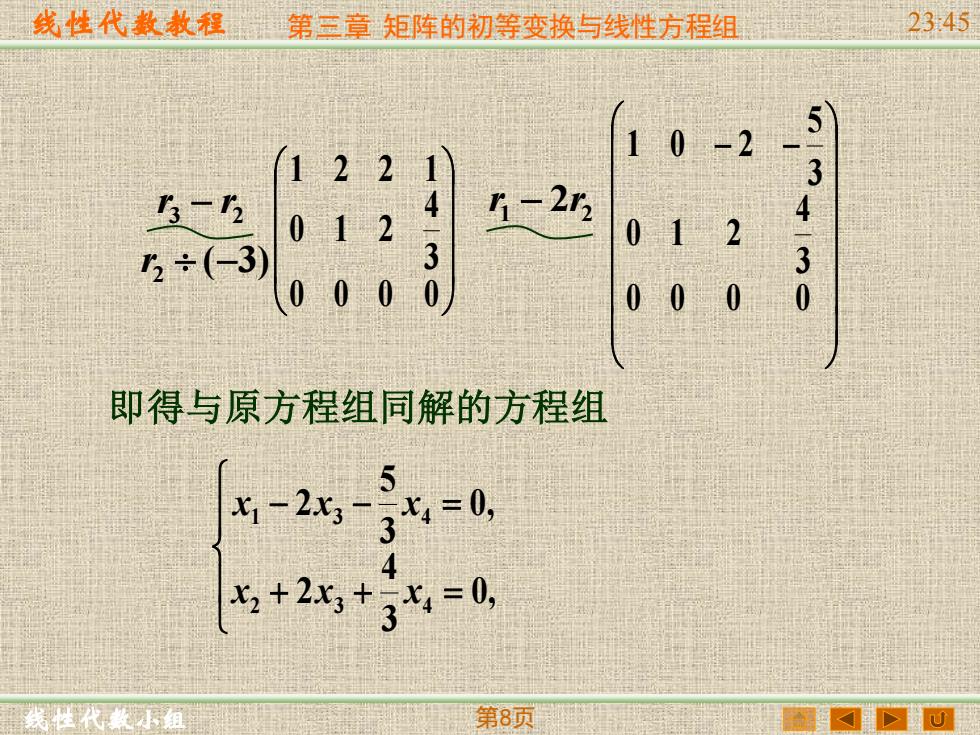
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第8页 0 0 0 0 3 4 0 1 2 1 2 2 1 ( 3) 2 3 2 - - r r r 1 2 2 r - r - - 0 0 0 0 3 4 0 1 2 3 5 1 0 2 即得与原方程组同解的方程组 + + = - - = 0, 3 4 2 0, 3 5 2 2 3 4 1 3 4 x x x x x x

线性代教教程■ 第三章矩阵的初等变换与线性方程组 2345 由此即得 4 =-2x,-34,(xx可任意取值. 令x=C1,x4=c2: 把它写成通常的参数形式 x1=2C2+ 5 3 2 4 39, -2 二C1 +C2 X3 x3=C1 X 0 x4=C2, 1 第9页
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第9页 = = = - - = + , , , 3 4 2 , 3 5 2 4 2 3 1 2 2 2 1 2 2 x c x c x c c x c c ( , ). x3 x4 可任意取值 由此即得 = - - = + , 3 4 2 , 3 5 2 2 3 4 1 3 4 x x x x x x 令 x3 = c1 , x4 = c2,把它写成通常的参数形式 . 1 0 3 4 3 5 0 1 2 2 1 2 4 3 2 1 + - - = c c x x x x