
曲顶柱体体积 V=J∬f(x,y)do D 平面薄片的质量M=∫f(x,y)do D 对二重积分定义的说明: ()二重积分的定义中,对闭区域的划分和 介点选取是任意的。 2) 当x,y)在闭区域上连续时,定义中和 腿 式的极限必存在,即二重积分必存在
曲顶柱体体积 = D V f (x, y)d 对二重积分定义的说明: = D 平面薄片的质量 M f (x, y)d (1) 二重积分的定义中,对闭区域的划分和 介点选取是任意的。 (2) 当 f(x , y )在闭区域上连续时,定义中和 式的极限必存在,即二重积分必存在
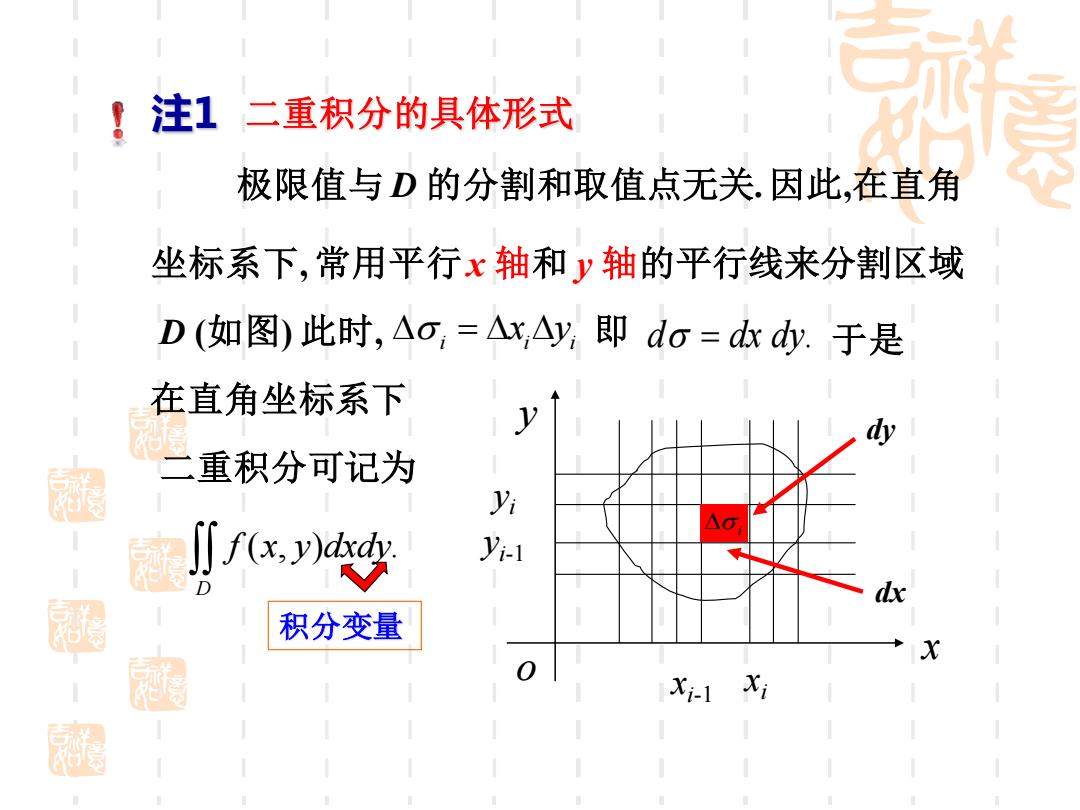
注1二重积分的具体形式 极限值与D的分割和取值点无关.因此,在直角 坐标系下,常用平行x轴和y轴的平行线来分割区域 D(如图)此时,Ao,=△x,Ay,即do=dkdy.于是 在直角坐标系下 二重积分可记为 yi f.yd yi-1 dx 积分变量 X Xi-1 Xi
极限值与 D 的分割和取值点无关. 因此,在直角 注1 坐标系下, 常用平行x 轴和 y 轴的平行线来分割区域 D (如图) 此时, i i i = x y 在直角坐标系下 二重积分可记为 ( , ) . D f x y dxdy 积分变量 即 d dx dy = . 于是 i xi-1 xi yi yi-1 x y o dx dy 二重积分的具体形式

注2二重积分只与被积函数和积分区域有关,而与 积分变量无关,即∬fx,y)ao=∬f,)do I注3若函数fK,y)在闭区域D上连续,则f化,y) 在D上可积.但是连续是可积的充分条件, 而非必要条件, 1注4 区域Aa的直径d是指d=POl, -秋私 程 #
二重积分只与被积函数和积分区域有关,而与 ( , ) ( , ) . D D f x y d f u v d = 积分变量无关, 即 注2 若函数 f (x, y)在闭区域D上连续,则f (x, y) 在 D上可积. 但是连续是可积的充分条件, 注3 注4 区域 的直径 d 是指 , max | |. P Q D d PQ = 而非必要条件. #