
第1章向量与坐标 §1.1向量的概念 1.下列情形中的向量终点各构成什么图形? (1)把空间中一切单位向量归结到共同的始点: (2)把平行于某一平面的一切单位向量归结到共同的始点: (3)把平行于某一直线的一切向量归结到共同的始点: (4)把半行于某一直线的一切单位向量归结到共同的始点, [解]:(1)单位球面: (2)单位圆 (3)直线: (4)相距为2的两点 2.设点O是正六边形ABCDEF的中心, 在向量OA、OB、OC、OD、OE、 OF、AB、BC、C⑦、D正、F B 和FA中,哪些向量是相等的? [解]:图1-1,在正六边形ABCDEF中, 相等的向量对是: 图1-1 OA和EF:OB和FA:OC和AB:OE和CD,OF和DE, 3.设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB.BC CD DA的中点,求证:KL=NM.当ABCD是空间四边形时,这等式是杏也成立? [证明]:如1图1-2,连结AC,则在△BAC中, 24C.K立与4C方向相同:布AD1C KL丛 中,NM丛AC.NM与AC方向相同,从而 KL=NM A.KL与NM方向相同,所以KL= NM. 4.如图1-3,设ABCD-EFGH是一个平行六面 体,在下列各对向量中,找出相等的向量和 B 互为相反向量的向量: (1)AB、CD:(2)AE、CG: (3) AC、EG: (4)AD、GF: (S)BE、Ca [解]:相等的向量对是(2)、(3)和(5): 图1—3 互为反向量的向量对是(1)和(4)。 §1.3 数量乘向量 1.要使下列各式成立,向量a,b应满足什么条件? )后+=6- (2)a+=+时 (3)后+=同- (4)后--同+

(5)--=日- [解]:(1)a,b所在的直线垂直时有a+--: (2)a.i同向时有6+=同+例 (3)同≥尽且a,6反向时有后+=- (4)a,6反向时有后-=日+ (5)a,b同向,1 同≥时有6-=同-风 2.设L、M、N分别是△ABC的三边BC、CA、AB的中点,证明:三中线向量AL BM CN 可以构成一个三角形 [证明]: AL=(4B+C) 所-+G CN =(CA+CB) :.AL+BM+CN=-(4B+4C+BA+BC+C4+CB)=0 从而三中线向量AL,BM,CN构成一个三角形。 3.设L、M、N是△ABC的三边的中点,O是任意一点,证明 OA+OB+OC=OL+OM+ON [证明]OA=OL+LA OB =OM+MB OC-ON+NC ..OA+OB+OC =OL+OM+ON+(LA+MB+NC) =OL+OM+ON-(AL+BM+CN) 山上题结论知:AL+BM+CN=0 ..0A+0B+OC=OL+OM+ON 4.用向量法证明,半行四边行的对角线互相兴分. [证明]:图1-4,在半行四边形ABCD中,O是对角线AC,BD的交点 D AD=OD-OA BC=OC-OB /0 但AD=BC ·.OD-OA=OC-OB 图1-4 OA+OC=OD+0B 山于(OA+OC)∥AC,(OB+OD)∥BD,而AC不半行于BD, ...0A+OC=OD+0B=0, 从而OA=OC,OB=OD
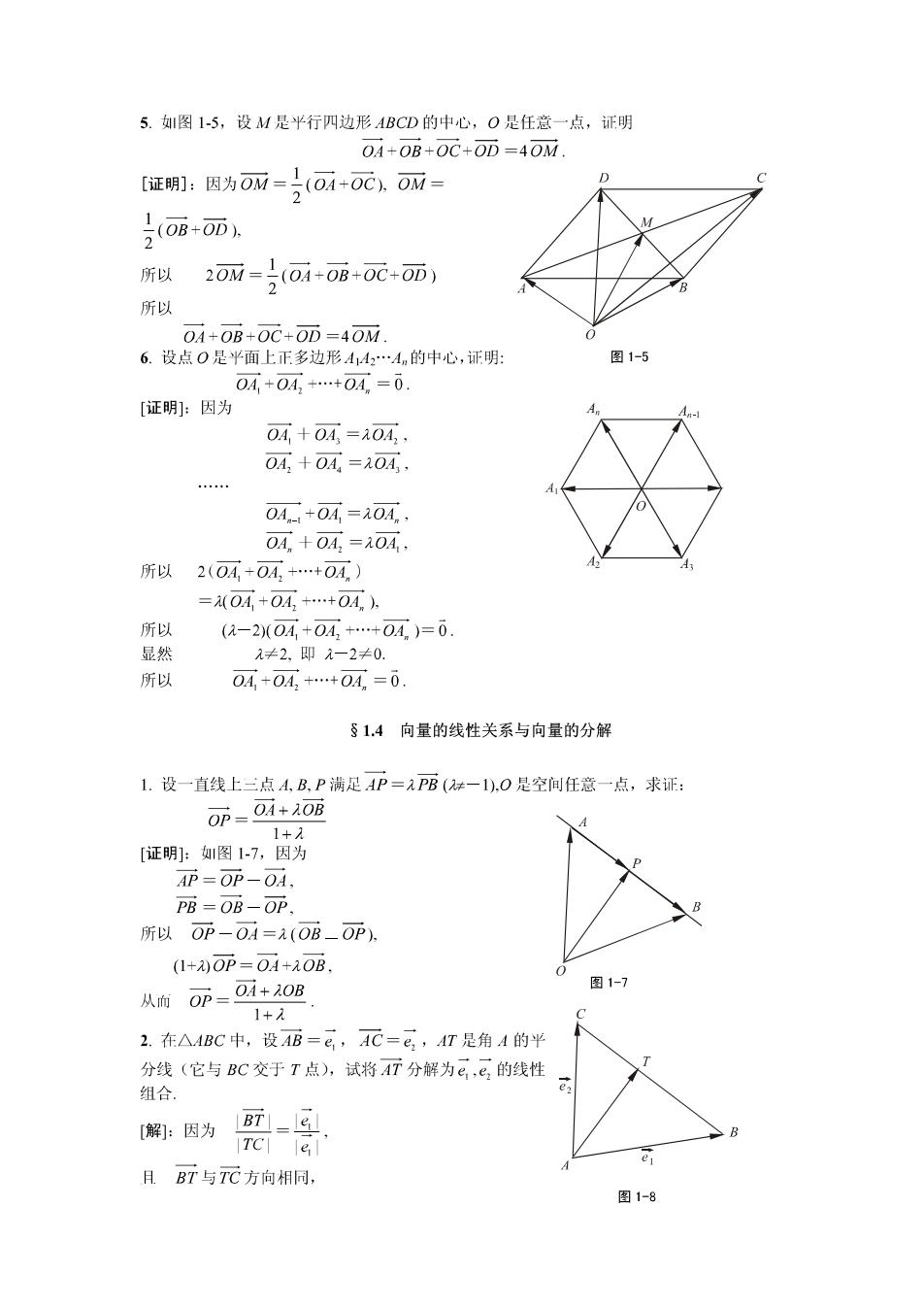
5.1图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明 0A+0B+0C+OD=40M [证明]:因为OM=(OA+0C,OM= 0 08-0 M 所以 20丽-0i+0+0元+0n, 所以 0A+0B+OC+OD =40M 0 6.设点O是平面上正多边形A142…An的中心,证明: 图1-5 OA,+OA2+…+OAn=0 [证明]:因为 OA+04,=104,, 0A,+0A=20A, *… 0An+0A=0A. OA,+04,=104,, 所以2(OA,+OA,++OA,) =(OA,+OA2+…+OA。)片 所以 (1-2(0A,+0A,+…+0A)=0 显然 ≠2.即元-2≠0. 所以 0A+0A,++0A=0 §1.4向量的线性关系与向量的分解 1.设一直线上三点A,B,P满足AP=元PB(+一1),O是空间任意一点,求证: 0p- OA+OB 1+ [证明]:图1-7,因为 AP=OP-OA, PB=OB-OP 所以OP-OA=(OB-OP). (1+)OP=04+1OB 从而 0p=O1+20B 图1-7 1+元 2.在△4BC中,设AB=e,AC=G,AT是角A的平 分线(它与BC交于T点),试将AT分解为e,C,的线性 组合 [解]:因为 BTe 月BT与TC方向相同, 图1-8

所以 B7=ST元 e 山上题结论有 e+ e -e, A7= e, le,le+lele, 1+19 le+le, e, 3.用向量法证明:P是△ABC重心的充要条件是 PA+PB+PC=0 [证明]:“三”若P为△ABC的重心,则 CP=2PE=PA+PB. 图1-9 从而PA+PB-CP=0. 即PA+PB+PC=0. “∈”若PA+PB十PC=0, 则PA+PB=一PC=CP 取E,F,G分别为AB,BC,CA之中点,则有 PE=(P4+PB). 从而CP=2PE. 同理可证BP=2PG,AP=2PF.故P为△ABC的重心. 4.证明三个向量a=-g,+3e,+2e,b=4e,-6e,+2e,c=-3e,+12e,+11g共面, 其中a能杏用b,c线性表示?能表示,写出线性表示关系式. [证明]:山于向量,e,g不共面,即它们线性无关. 考虑表达式a+ub+vc=0,即 1(-e+3e+2e)+u(4e,-6e,+2e,)+v(-3e,+12e十11e)=0, 或(-2+4-3v)e,+(32-6u+12)e2+(2+2u+11)e=0. 山于e,,g线性无关,故有 -1+44-3y=0, 31-6十12y=0, 2元+24+11v=0. 解得2=-10,u=-1,v=2. 山于1=一10≠0,所以ā能用b,c线性表示 a=-05+5 10 5.图1-10,OA,OB,OC是二个两两不共线的向量,月OC=OA+uOB,试证A,B,C 三点共线的充要条件是+u=1. B [证明]:“→”因为A,B,C共线,从而有 AC//CB. 月有m≠一1,使AC=mCB, OC-OA=m (OB-OC). (1+m)OC=0A+mOB, 图1-10

0c=,101+,m0B 1+m 1+m 但已知OC=1OA+uOB.山OC对OA,OB分解的唯一性可得 ≈、1 、n 1+m 1+m 1+m=1. 从而左4一十m1+m “=”设+u=1.则有OC=OA十uOB=AOA十(1-)OB =OB+(OA-OB). OC-OB=(OA-OB), 所以BC=1BA」 从而BC∥BA. 故A,B,C三点共线。 §1.5标架与坐标 1.在空间直角坐标系{O:i,j,k}下,求P(2.一3,一1),Ma.b,c)关于 (1)坐标平面:(2)坐标轴:(3)坐标原点的各个对称点的坐标. [解]:M(a,b,c)关于xOy平面的对称点坐标为(a,b,一c), M(a,b,c)关于yOz平面的对称点坐标为(一a,b,c), M(a,b,c关于xOz半面的对称点坐标为(a,一b.c), M(a,b,c)关于x轴平面的对称点坐标为(a,一b,一c), M(a,b,c)关于y轴的对称点的坐标为(一a,b,一c), M(a,b,c)关于z轴的对称点的坐标为(一a,一b,c). 类似考虑P(2,-3,-1)即可. 2.已知向量a,b,c的分量如1下: (1)a={0,-1,2,i=0,2,-4},c={1,2,-1: (2)a={1,2,3},b={2,-1,0},c={0,5,6. 试判别它们是杏共面?能杏将c表成a,b的线性组合?若能表示,写出表示式. 0-1 2 [解](1)因为 02 -4 0.所以a,6,c三向量共面, 1 2 -1 又因为a,b的对应坐标成比例,即a1b,但c次a, 故不能将c表成a,b的线性组合 123 (2)因为2-10=0.所以a,6,c三向量共面 056 又因为a,方的对应坐标不成比例,即a石, 故可以将c表成a,b的线性组合. 设c=ā+ub,亦即{0,5,6}={1,2,3}+{2,一1,0} 从而