
类似可定义 ∬P(x,yz)k=lm∑P(5,n,5,AS,) 2→0 i1 称为P(化,3,)在有向曲面∑上对”,z的曲面积分; ∬x,zt=m∑(5,n,5△s)x 2-→0 i=1 称为Q(化,y,)在有向曲面∑上对乙,x的曲面积分;
类似可定义 ∫∫ ∑ = → Σ = Δ n i P i i i Si yz P x y z dydz 1 0 ( , , ) lim (ξ ,η ,ζ )( ) λ ∫∫ ∑ = → Σ = Δ n i dzdx Q i i i Si zx Q x y z 1 0 ( , , ) lim (ξ ,η ,ζ )( ) λ 称为P (x, y, z)在有向曲面∑上对 y, z 的曲面积分; 称为Q (x, y, z)在有向曲面∑上对 z , x 的曲面积分;
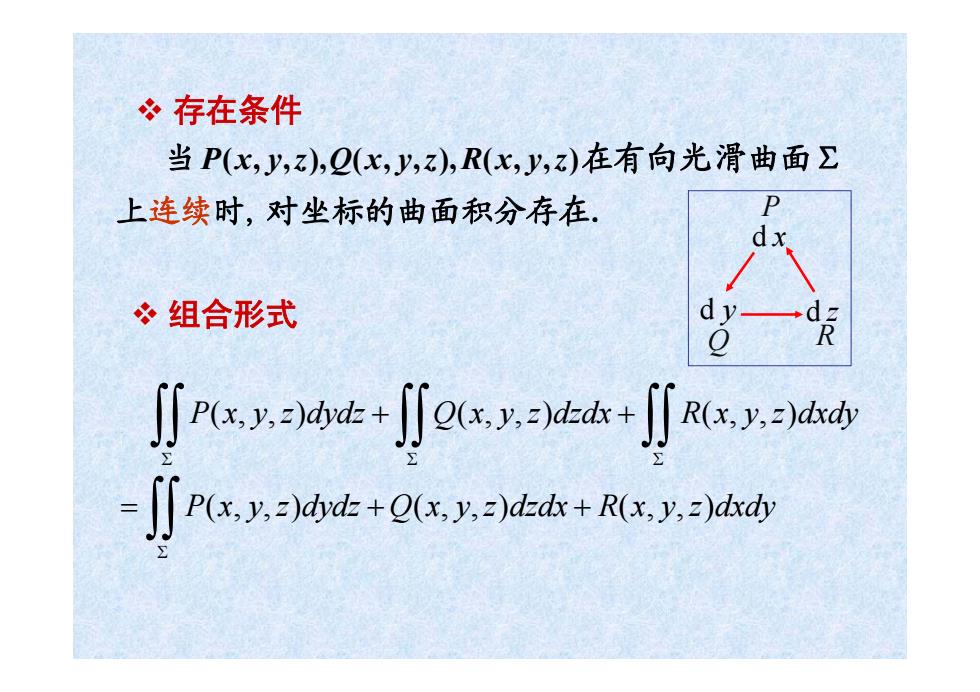
冬存在条件 当P(x,Jy,z),2(x,y,z),R(x,y,z)在有向光滑曲面∑ 上连续时,对坐标的曲面积分存在 冬组合形式 ∬ [JP(*.y.-)dvd-+Q(x.y.)d-ds+R(x.y.-)dsdy
d x d y d z P Q R P x y z dydz Q x y z dzdx R x y z dxdy (, ,) (, ,) (, ,) Σ = ++ ∫∫ 存在条件 当 P ( x , y , z), Q ( x , y , z), R ( x , y , z )在有向光滑曲面Σ 上连续 时, 对坐标的曲面积分存在. 组合形式 P x y z dydz Q x y z dzdx R x y z dxdy (, ,) (, ,) (, ,) ΣΣΣ + + ∫∫ ∫∫ ∫∫