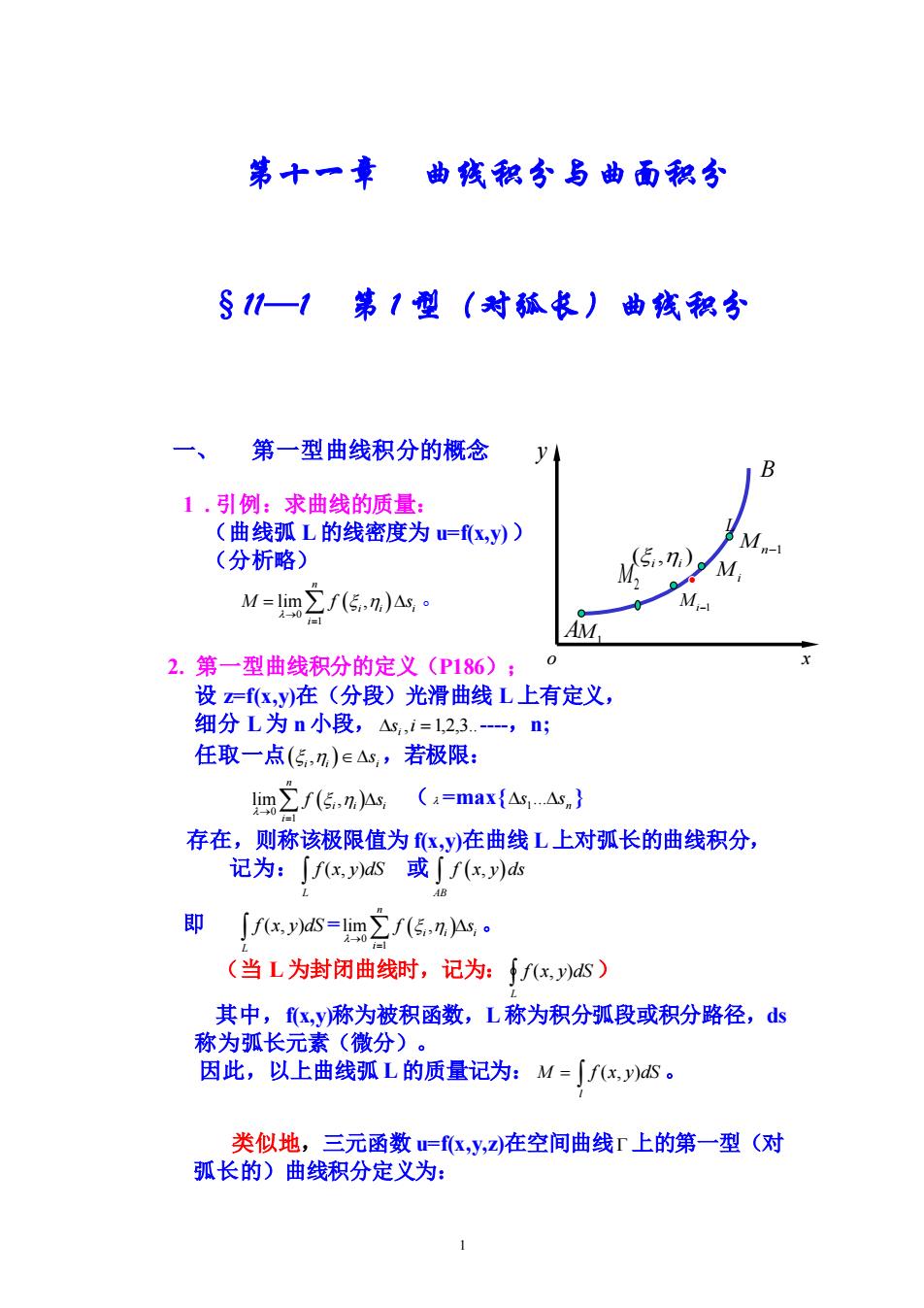
第十一章 曲钱积分与曲面积分 §1一1第1型(对蘸长)曲线积分 一、 第一型曲线积分的概念 1.引例:求曲线的质量 (曲线弧L的线密度为=xy)) (分析略) )小 M, M=m2fG,n)A。 M. AM, 2.第一型曲线积分的定义(P186); 设=k,y)在(分段)光滑曲线L上有定义, 细分L为n小段,△,i=1,2,3-,n 任取一点(5,n)e△s,若极限: lm∑f(5,n)As(=max{As△,} 存在,则称该极限值为x,y)在曲线L上对弧长的曲线积分, 记为:∫fx,s或∫fx)杰 即∫fx,s=m∑f(传nAs· (当L为封闭曲线时,记为:∫/xs) 其中,fy称为被积函数,L称为积分弧段或积分路径,ds 称为孤长元素(微分)。 因此,以上曲线弧L的质量记为:M=∫fx,ys。 类似地,三元函数=fx,y,z)在空间曲线Γ上的第一型(对 弧长的)曲线积分定义为:
1 第十一章 曲线积分与曲面积分 §11—1 第 1 型(对弧长)曲线积分 一、 第一型曲线积分的概念 1 . 引例:求曲线的质量: (曲线弧 L 的线密度为 u=f(x,y) ) (分析略) ( ) 0 1 lim , n i i i i M f s → = = 。 2. 第一型曲线积分的定义(P186); 设 z=f(x,y)在(分段)光滑曲线 L 上有定义, 细分 L 为 n 小段, s ,i =1,2,3. i -,n; 任取一点 ( i i , ) i s ,若极限: ( ) 0 1 lim , n i i i i f s → = ( =max{ n s .s 1 } 存在,则称该极限值为 f(x,y)在曲线 L 上对弧长的曲线积分, 记为: L f (x, y)dS 或 ( , ) AB f x y ds 即 L f (x, y)dS = ( ) 0 1 lim , n i i i i f s → = 。 (当 L 为封闭曲线时,记为: L f (x, y)dS ) 其中,f(x,y)称为被积函数,L 称为积分弧段或积分路径,ds 称为弧长元素(微分)。 因此,以上曲线弧 L 的质量记为: M = l f (x, y)dS 。 类似地,三元函数 u=f(x,y,z)在空间曲线 上的第一型(对 弧长的)曲线积分定义为: A B o x y M2 M1 Mi−1 Mi M n−1 ( , ) i i L

达=2/) 二、第一型曲线积分的性质: 1、∫kxy)dS=k∫fx,y)dS,(k为常数): 2、「f+gds=「fds±「gds, 3、「fds=∫as+∫fas: 4∫/,S=∫f3,y心,(对弧长的曲线积分与曲线的方 向无关!这也是对弧长积分与对坐标积分的主 要区别) 三、对弧长曲线积分的计算方法: (化为定积分求解法,但转化时要注意一上限>下限) 1若曲线L的方程为参数方程x=% ,(a≤t≤B):且 y=9() g(0与g(0)连续,则: Jr.yd=().(+(d 由上册可知弧长微分元素为 ds-)+(d)()+((d 2、若曲线1的方程为y=x,(a≤x≤b),y(x)连续, 则: [fx,y达=fx,xN1+y2 若曲线1的方程为x=g(y),(c≤y≤d 则 ∫fxy)s=f[g(y),y]V1+(x) x=p(0 3、(空间曲线)若r的方程为:y=()(a≤1≤B) 二=03(1)
2 ( ) ( ) 0 1 , , lim , , n i i i i i f x y z ds f s → = = 二、 第一型曲线积分的性质: 1、 l kf(x, y)dS =k l f (x, y)dS , (k 为常数); 2、 + l ( f g)dS = l fdS l gdS ; 3、 = 1+ 2 l l l fdS = 1 l fdS + 2 l fdS ; 4、 AB f (x, y)dS = BA f (x, y)dS ,(对弧长的曲线积分与曲线的方 向无关!-这也是对弧长积分与对坐标积分的主 要区别) 三、 对弧长曲线积分的计算方法: (化为定积分求解法,但转化时要注意-上限 下限) 1.若曲线 L 的方程为参数方程 ( ) ( ) 1 2 x t y t = = ,( t );且 ( ) ( ) ' ' 1 2 t t 与 连续,则: l f (x, y)dS = ( ) ( ) ( ) ( ) ' 2 ' 2 1 2 1 2 f t t t t dt , ( ) ( ) + 由上册可知弧长微分元素为 ds= ( ) ( ) ( ( )) ( ( )) 2 2 2 2 ' ' 1 2 dx dy t t dt + = + 2、若曲线 l 的方程为 y = y(x),(a x b), y'(x) 连续, 则: f x y ds f x y x y dx b l a 2 ( , ) = ( , ( )) 1+ ( ') 若曲线 l 的方程为 x g y c y d = ( ),( ) ; 则 l f (x, y)dS = ( ) ( ) 2 ' , 1 d c f g y y x dy + 3、(空间曲线)若 的方程为: = = = ( ) ( ) ( ) 3 2 1 z t y t x t ( t )

则∫f(xy)d达=∫f(m,g))+(p+(g)d山 例1):(189页-例1), 例2):(190页-3(4)题) 例3):(189页-例3) 例4): 求=x+y+:-)杰,其中:「是从点A,2,-)到点8(2-1)的直线。 四、应用 1、 几何上,求弧长:s=[=V1+y)山 2、 物理上:求曲线的质量M=[fx,y)达(f(x,y)为线度) 重心(x,习) =xns,=列恤 转动惯量↓,=∫y2fx,)d山 1,=[x'f(x.y)ds 1=(x+y)f(x.y)ds 例5):(190页-一4题) 作业:(190页-1(3).5),7题)
3 则 ( ) ( ) ( ) ( ) ( ) 2 2 2 ' ' ' 1 2 3 1 2 3 f x y z ds f dt , , , , = + + 例 1):(189 页-例 1), 例 2):(190 页-3(4)题) 例 3):(189 页-例 3) 例 4): I x y z ds B ( 1 , 2, 1,1 ) ( ) ( ) = + + − − 求 其中: 是从点A 1,2,-1 到点 的直线。 四 、应用 1、 几何上,求弧长: s ds y dx b l a = = + 2 1 ( ') 2、 物理上:求曲线的质量 = l f (x, y)ds ( f (x, y) 为线度) 重心 ( x y, ) = l xf x y M x ( , ) 1 ds , ( ) 1 , l y yf x y ds M = 转动惯量 = l I x y f (x, y)ds 2 = l I y x f (x, y)ds 2 ( ) ( ) 2 2 0 , l I x y f x y ds = + 例 5):(190 页-4 题) 作业:(190 页-1(3),(5),(7)题)
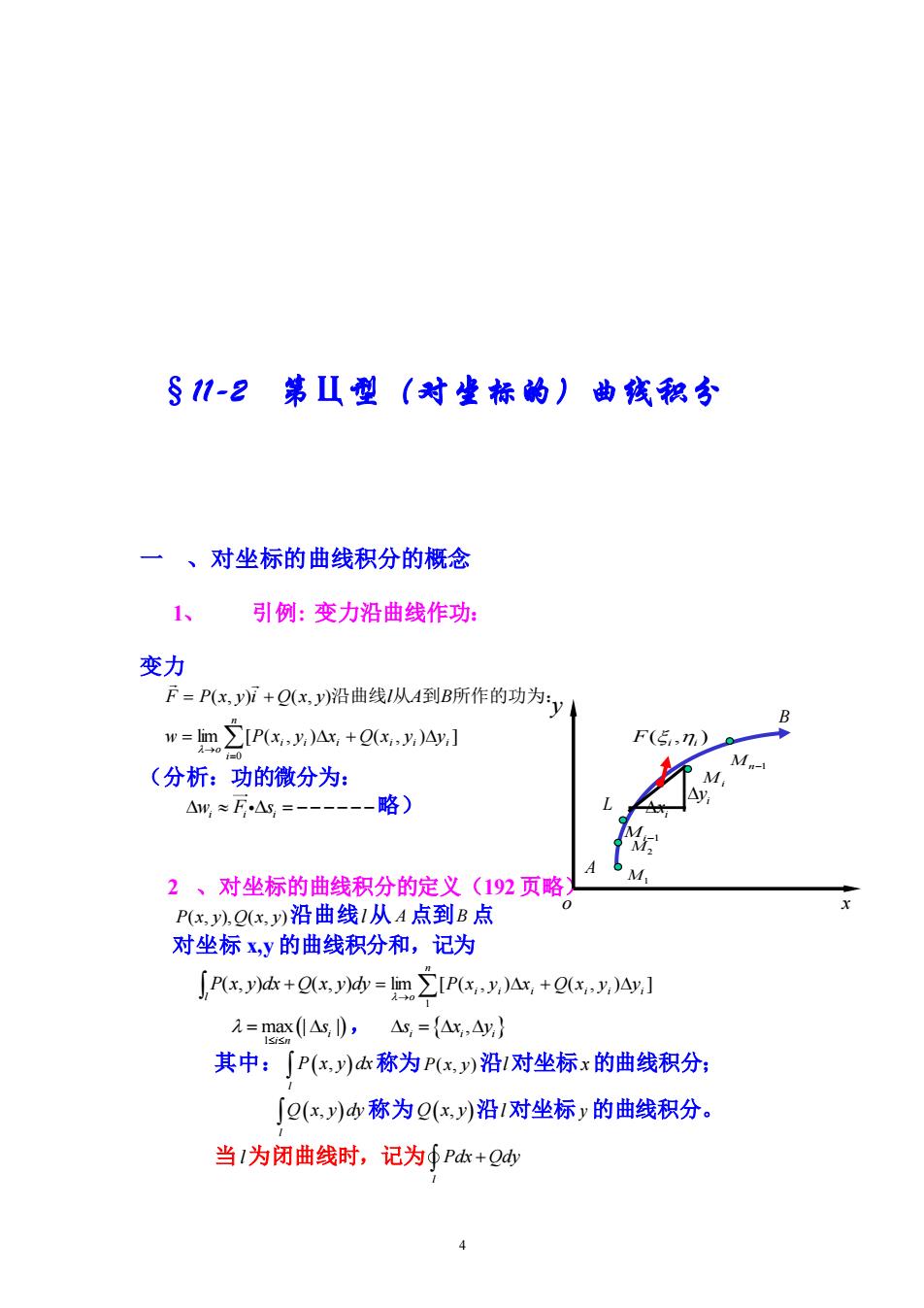
§-2第山型(对业标的)曲线积分 一、对坐标的曲线积分的概念 1、引例:变力沿曲线作功: 变力 =Px,7+Q(x,)沿曲线从A到B所作的功为:y w=m∑[P(x,y)△x,+Qx,y,)Ay,] F(5,n,) (分析:功的微分为: M -略) M. 2、对坐标的曲线积分的定义(192页略) P(x,以,Q(x,)沿曲线1从A点到B点 对坐标x,y的曲线积分和,记为 .()A+(x)v] 元=max0As0,△s,={Ax,4y} 其中:∫P(x,)称为Px)沿1对坐标x的曲线积分: ∫Q(xy)称为Q(x,y)沿/对坐标y的曲线积分。 当1为闭曲线时,记为∮P本+Q
4 §11-2 第Ц型(对坐标的)曲线积分 一 、对坐标的曲线积分的概念 1、 引例: 变力沿曲线作功: 变力 F = P(x, y)i + Q(x, y)沿曲线l从A到B所作的功为: = → = + n i i i i i i i o w P x y x Q x y y 0 lim [ ( , ) ( , ) ] (分析:功的微分为: = − − − − − − w F s i i i 略) 2 、对坐标的曲线积分的定义(192 页略) P(x, y),Q(x, y) 沿曲线 l 从 A 点到 B 点 对坐标 x,y 的曲线积分和,记为 P x y dx Q x y dy l ( , ) + ( , ) = + → n i i i i i i o P x y x Q x y y 1 lim [ ( , ) ( , ) ] ( ) 1 max | | i i n s = , = s x y i i i , 其中: ( , ) l P x y dx 称为 P(x, y) 沿 l 对坐标 x 的曲线积分; ( , ) l Q x y dy 称为 Q x y ( , ) 沿 l 对坐标 y 的曲线积分。 当 l 为闭曲线时,记为 l Pdx Qdy + o x y A B L ( , ) F i i M1 M2 Mi−1 Mi M n−1 i x i y

(因此,以上作功问题记为w=P本+Q) 类似地,定义三元函数Px,以0(x,男x,y,)沿曲线Γ对坐 标x5,:的曲线积分和为: Pk+Q+Rt即 ∫Px,y)=lim∑P5,n,5)△x ∫Q(x,y=lim∑0(5,n,5,)Ay JRx,yt=m∑R5,n,5)△ 二、对坐标曲线积分的性质一一类似对弧长的曲线积分性质, 但有一点不同的是: ∫.Pt+Q=-JPt+Q 三、对坐标曲线积分的计算方法(化为定积分计算时,要求定 积分的下、上限与曲线的始点、终点分别对应) 、若1为参数方程0(从a→0):且,0连续。 y=p2() 则∫Px本+Oxy=Pm,)9+00,0)n,'h (194-195页证明) 2.若1的方程为y=y(x),(x从a→b),且y(x)连续, 则Pxy+Qx,=P(x,x》+Qx,x》门 3.若1的方程为x=o(y.O从c→d,且0(y)连续 则∫Px,y)d+Qx,y)=[Po(x,小pyy'+I(y%x] x=9,) 4.若空间曲线r方程为:y=p,()(从a→B) e=p,0 则∫P(x,y)s=P(a%gmh ∫0(x,y)y=∫Q(g,9,%p,t R(x.y.-)d=R()d
5 (因此,以上作功问题记为 = + l w Pdx Qdy ) 类似地,定义三元函数 P(x, y,z),Q(x, y,z), R(x, y,z) 沿曲线 对坐 标 x, y,z 的曲线积分和为: Pdx + Qdy + Rdz 即 二 、对坐标曲线积分的性质-类似对弧长的曲线积分性质, 但有一点不同的是:- + = − + AB BA Pdx Qdy Pdx Qdy 三 、对坐标曲线积分的计算方法(化为定积分计算时,要求定 积分的下、上限与曲线的始点、终点分别对应) 1、若 l 为参数方程 = = ( ) ( ) 2 1 y t x t ( t从 → );且 ( ), ( ) ' 2 ' 1 t t 连续。 则 P x y dx Q x y dy P Q dt l + = + ( , ) ( , ) [ ( , ) ' ( , ) '] 1 2 1 1 2 2 (194-195 页证明) 2.若 l 的方程为 y y x x a b y x = → ( ),( ), ( ) 从 且 ’ 连续, 则 + = + • b a P(x, y)dx Q(x, y)dy [P(x, y(x)) Q(x, y(x)) y(x) ]dx 3.若 l 的方程为 x= (y). ( ) ' ( ), y c d y 从 → 且 连续 则 + = • + d c P(x, y)dx Q(x, y)dy [P[(x), y] (y) Q[(y), x]dy 4. 若空间曲线 方程为: = = = ( ) ( ) ( ) 3 2 1 z t y t x t ( t从 → ) 则 ( ) ( ) ' 1 2 3 1 P x y z dx P dt , , , , = ( ) ( ) ' 1 2 3 2 Q x y z dy Q dt , , , , = ( ) ( ) ' 1 2 3 3 R x y z dz R dt , , , , = 0 1 ( , , ) lim ( , , ) . n i i i i i P x y z dx P x → = = 0 1 ( , , ) lim ( , , ) . n i i i i i Q x y z dy Q y → = = 0 1 ( , , ) lim ( , , ) . n i i i i i R x y z dz R z → = =