
第九章多元高数的散分法 §9-1 多元画数的報限及连续 上、多元函数的概念 1.几个概念 1)邻域-一N(x,e)={x小-xke到(开区间 N(P。,E)-{xy)1(x-x。)2+y-y。)2<62}(开圆) NM,s)={Ky1K-xo)2+y-y)2+(E-)》2<82}(开球) 2)区域-一由一条或几条平面曲线围成的部分平面,称为平面 区域;围成平面区域 的曲线称为区域的边界:(不)包含边界的区域称(开)闭区(不) 能用半径为有限值的圆包围的区域称为(无界)有界区域。 (内点,开集,聚点等略) 3)连通区域-一若区域D内任两点,都可用折线联结起来,且该 折线上的点都属于D 的区域。分为单连通区域-一没有洞的 复连通区域-一有洞的 2.多元函数的概念(56页) (二元函数)=fk,y)(Ky)eD (有两个自变量) (三元函数)4=fx,y,) (有三个自变量) (元函数)μ=fx,x2,x3xn) (有n个自变量) 称二元以及二元以上的函数为多元函数二元函数x,y)的图形 是一个曲面(如图)
1 第九章 多元函数的微分法 §9-1 多元函数的极限及连续 一、多元函数的概念 1. 几个概念 1)邻域- ( , ) { | | } ( ) N x0 = x x − x0 开区间 N(P , ) {(x, y) | (x - x ) (y - y ) } ( ) 2 2 0 2 0 = 0 + 开圆 N(M , ) {(x, y, z) | (x - x ) (y - y ) ( ) } ( ) 2 2 0 2 0 2 0 = 0 + + z − z 开球 2)区域-由一条或几条平面曲线围成的部分平面,称为平面 区域; 围成平面区域 的曲线称为区域的边界;(不)包含边界的区域称(开)闭区(不) 能用半径为有限值的圆包围的区域称为(无界)有界区域。 (内点,开集,聚点等略) 3)连通区域-若区域 D 内任两点,都可用折线联结起来,且该 折线上的点都属于 D 的区域。分为 −−−−− −−−−− 单连通区域 没有洞的 复连通区域 有洞的 2. 多元函数的概念 (56 页) (二元函数) z=f(x,y) (x,y) D (有两个自变量) (三元函数) = f (x, y,z) (有三个自变量) (n元函数) ( , , ,. ) 1 2 3 n = f x x x x (有n个自变量) 称二元以及二元以上的函数为多元函数 二元函数 z=f(x,y)的图形 是一个曲面(如图)
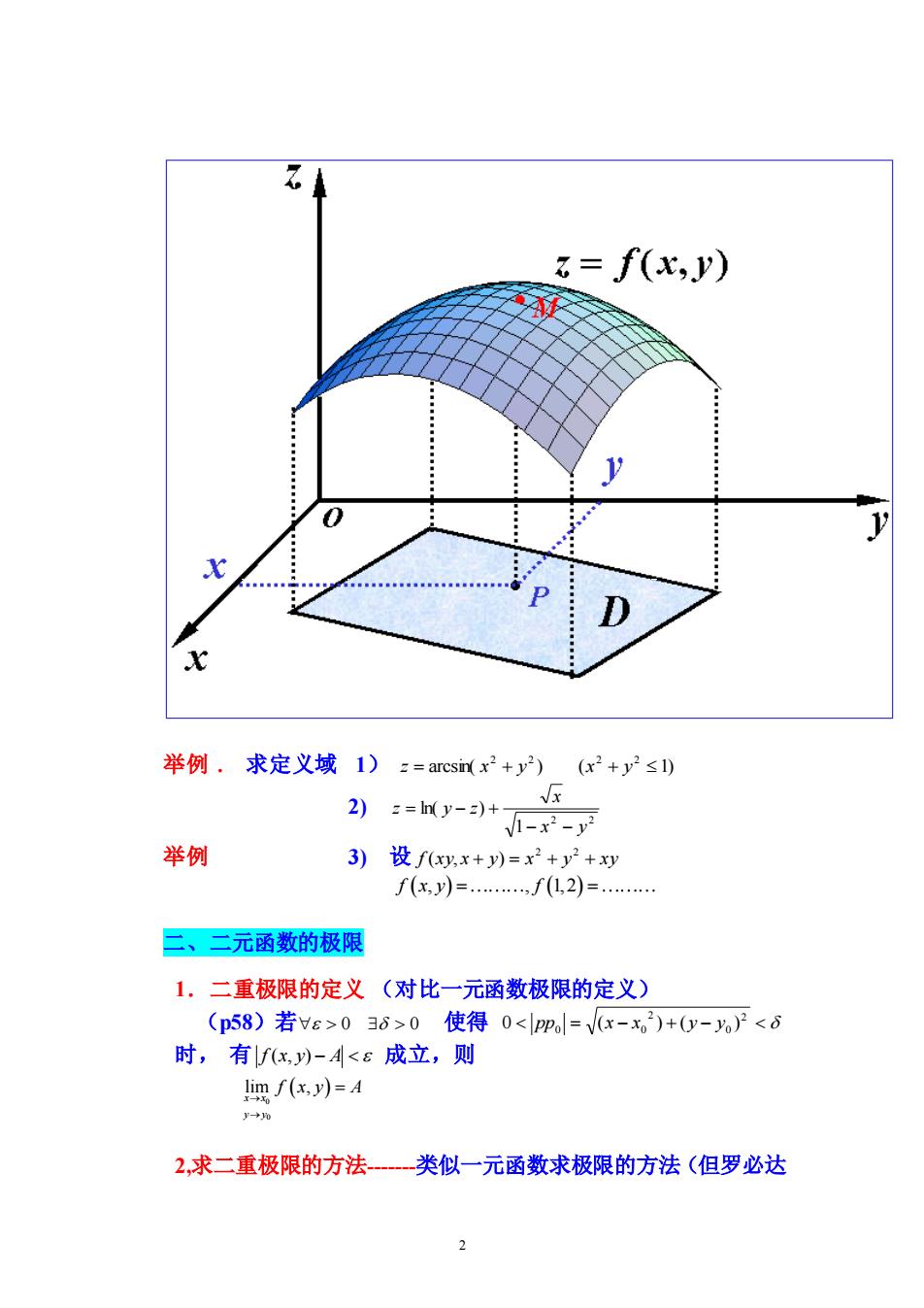
=f(x,y) 举例.求定义域1)z=aresinx2+y2)(x2+y2≤1) 2)s=n(y-)+ -x2-y 举例 3)设fxyx+y)=x2+y2+xy f(xy)=.,fL,2)= 二、二元函数的极限 1.二重极限的定义(对比一元函数极限的定义) (p58)若∀6>036>0使得0<ppl=V(x-x,2)+y-)2<8 时,有/x,)-<E成立,则 lim f(x.y)=4 → 2,求二重极限的方法一类似一元函数求极限的方法(但罗必达 2
2 举例 . 求定义域 1) arcsin( ) ( 1) 2 2 2 2 z = x + y x + y 2) 2 2 1 ln( ) x y x z y z − − = − + 举例 3) 设 f xy x + y = x + y + xy 2 2 ( , ) f x y f ( , , 1,2 ) = = ( ) 二、二元函数的极限 1.二重极限的定义 (对比一元函数极限的定义) (p58)若 0 0 使得 = − + − 2 0 2 0 0 0 pp (x x ) (y y ) 时, 有 f (x, y) − A 成立,则 ( ) 0 0 lim , x x y y f x y A → → = 2,求二重极限的方法-类似一元函数求极限的方法(但罗必达

法则不能用于求二重极限) 举例-1) 2-xy+4 2) cos 3)1im(1+y)F 3.证明- imxy)不存在,往往采用2种方法之一 「方法一设y=kx和y=k,x分别求出mlxy)的值,若其值不同,则lmxy)不存在 方法二设y=kx求mfxy)=pk),证明不存在 举例4)证:m+少不存在 x-y 三。二元函数的连续(对比一元函数连续定义讲) 设f(x,)在(p)内有定义 若会月=W》@=0,则称y在点() 连续。 若fk,y)在D内每一点都连续,则称fx,y)在D内是连续的。 连续的性质一与一元函数连续的性质类同如: 一切多元函数在定义域所对应的区域内都连续。 连续不极限存在 作业-63页第6(4)、7(2) §9-2偏导数 二、偏导数的定义(64页)
3 法则不能用于求二重极限) 举例- 1) xy xy y x 2 4 lim 0 0 − + → → 2) xy x y y x 1 lim ( ) cos 2 2 0 0 + → → 3) ( ) 1 0 2 lim 1 x x y xy → → + 3.证明- limf(x, y)不存在,往往采用2种方法之一 = = = = y kx, limf(x, y) (k), . x y k limf(x, y) limf(x, y) . 1 2 方法二 设 求 证明不存在 方法一 设 和 分别求出 的值,若其值不同,则 不存在 y k x 举例 4) 证: 不存在 x y x y y x − + → → 0 0 lim 三. 二元函数的连续(对比一元函数连续定义讲) 设 f x y ( , )在U p( 0 )内有定义 若 lim ( , ) ( , ) (or lim z 0) , y 0 x 0 0 0 x x 0 0 = = → → → → f x y f x y y y 则称 f(x,y)在点( 0 0 x , y ) 连续。 若 f(x,y)在 D 内每一点都连续,则称 f(x,y)在 D 内是连续的。 连续的性质—与一元函数连续的性质类同.如: 一切多元函数在定义域所对应的区域内都连续。 连续 ⎯⎯⎯ ⎯⎯⎯→ 一定 不一定 极限存在 作业-63 页第 6(4)、7(2) §9-2 偏 导 数 一、 偏导数的定义(64 页)

设f(x,y)在U(®,)内有定义,若极限 一化+A,存在,则称该极限值为:=化)在点 对x的偏导数,记为f.(x,)或 会ln或lw 即w)=巴+A)- 类似地,定义:=fx,y)在点(x,)对y的偏导数为 f6,)=典出+4)-fx 此时,也称:=x,)在(x)点可导,否则称不可导。 同理,定义:=fx,)对x,y的两个偏导函数(简称为偏导数)为 f(x.y)=lim f(x+△x,y)-f(x,y) △x 或记为察、或 =典y+0》或记为等、哥或 △ 偏导函数的定义类似地可以推广到三元函数以上。 例1)讨论了化=F平列=(00)在(0,0)点的可导性。 0.(x,y)=(0,0) 二、偏函数的求法 求一个多元函数对某个自变量的偏导数时,只要把其他的自变 量视为常数,而对所讨论的自变量利用一元函数的求导公式、法则进 行求导便可。即 器-孟川一少视为常数: 年川—视:为常 数。 类似地可以推广到三元函数以上的偏导数求法, 举例:2)x)=2xy+csy+-smx+2y。求00 3)f,m=2r2+0-)aresin+e。求0,)及.财(0,1) (求下列偏导数)
4 设 f x y ( , )在U p( 0 )内有定义 ,若极限 x f x x y f x y x + − → ( , ) ( , ) lim 0 0 0 0 0 存在,则称该极限值为 z = f (x, y) 在点 ( , ) 0 0 x y 对 x 的偏导数,记为 ( , ) 0 0 ' f x x y 或 ( , ) 0 0 | x y x z 或 ( , ) ' 0 | x x y o z 即 x f x x y f x y f x y x x + − = → ( , ) ( , ) ( , ) lim 0 0 0 0 0 0 0 ' 类似地,定义 ( , ) ( , ) 0 0 z = f x y 在点 x y 对 y 的偏导数为 y f x y y f x y f x y y y + − = → ( , ) ( , ) ( , ) lim 0 0 0 0 0 0 0 ' 此时,也称 z = f (x, y) 在 ( x y 0 0 , ) 点可导,否则称不可导。 同理,定义 z = f (x, y) 对 x, y 的两个偏导函数(简称为偏导数)为 x f x x y f x y f x y x x + − = → ( , ) ( , ) ( , ) lim 0 ' 或记为 x z 、 x f 或 ' x z y f x y y f x y f x y y y + − = → ( , ) ( , ) ( , ) lim 0 ' 或记为 y z 、 y f 或 ' y z 偏导函数的定义类似地可以推广到三元函数以上。 例 1) 讨论 ( ) ( ) ( ) ( ) ( ) 2 2 , , 0,0 , 0, , 0,0 xy x y f x y x y x y = + = 在(0,0)点的可导性。 二、偏函数的求法 求一个多元函数对某个自变量的偏导数时,只要把其他的自变 量视为常数,而对所讨论的自变量利用一元函数的求导公式、法则进 行求导便可。即 f (x, y) dx d x z = - y 视为常数; f (x, y) dy d y z = -视 x 为常 数。 类似地可以推广到三元函数以上的偏导数求法。 举例:2) f x y x y e y x y x ( , ) 2 cos sin 2 2 = + + + 。求 0, 0, 2 2 x y f f 及 3) y e y x f (x, y) = 2x + ( y −1) arcsin + 2 。求 f f x y (0,1 0,1 )及 ( ) (求下列偏导数)
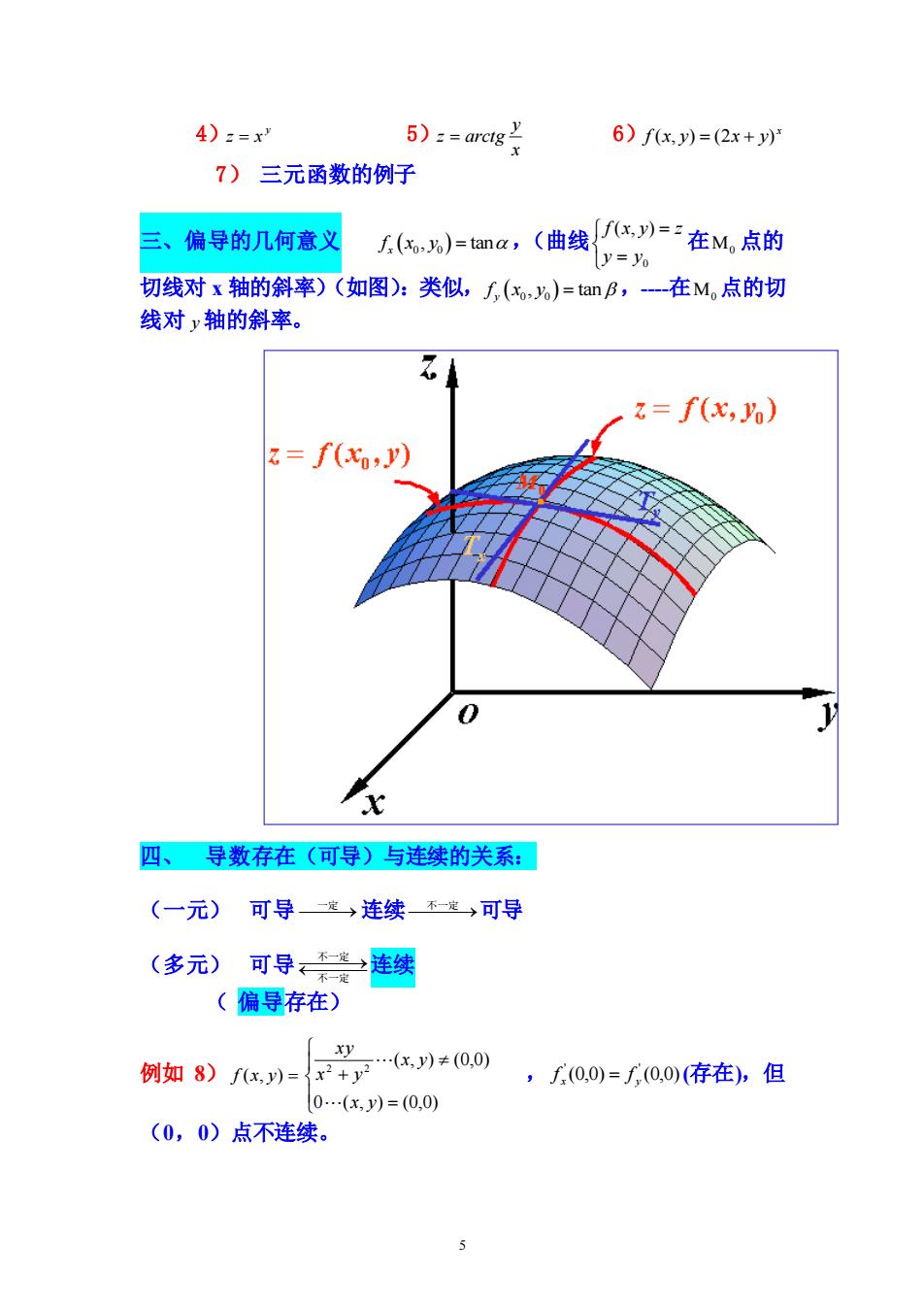
4)z=x 5)==arctg 6)fx,y)=(2x+y) 7)三元函数的例子 三、偏导的几何意义 Ek为)=ama,(曲线/)=F在M,点的 y=% 切线对x轴的斜率)(如图):类似,f(,)=anB,-在M,点的切 线对y轴的斜率。 z=f(x,yo) 3=f(x,) 0 四、导数存在(可导)与连续的关系:】 (一元)可导龙连续一可导 (多元)可导之连绣 (偏导存在) xy 例如8)任m=+少任川*00) ,f(0,0)=∫(0,0(存在),但 0.(x,y)=(0,0) (0,0)点不连续
5 4) y z = x 5) x y z = arctg 6) x f (x, y) = (2x + y) 7) 三元函数的例子 三、偏导的几何意义 f x y x ( 0 0 , tan ) = ,(曲线 = = 0 ( , ) y y f x y z 在 0 点的 切线对 x 轴的斜率)(如图):类似, f x y y ( 0 0 , tan ) = ,-在 0 点的切 线对 y 轴的斜率。 四、 导数存在(可导)与连续的关系: (一元) 可导 ⎯⎯⎯→ 一定 连续 ⎯⎯⎯→ 不一定 可导 (多元) 可导 ⎯⎯⎯ ⎯⎯⎯→ 不一定 不一定 连续 ( 偏导存在) 例如 8) f (x, y) = = + 0 ( , ) (0,0) ( , ) (0,0) 2 2 x y x y x y xy , (0,0) (0,0) ' ' x y f = f (存在),但 (0,0)点不连续