一、曲线拟合1曲线拟合问题的提法:已知一组(二维)数据,即平面上的n个点xi,yi),i=1,2,L,n,x互不相同,(曲线)y=f(x)寻求一个函数使f(x)在某种准则下与所有数据点最为接近,即曲线拟合最好,如图:(x;,J,)确定f(x)使得nnad, =a[f(x)- yPJ= f(x)i=1i=1达到最小+x最小二乘准则
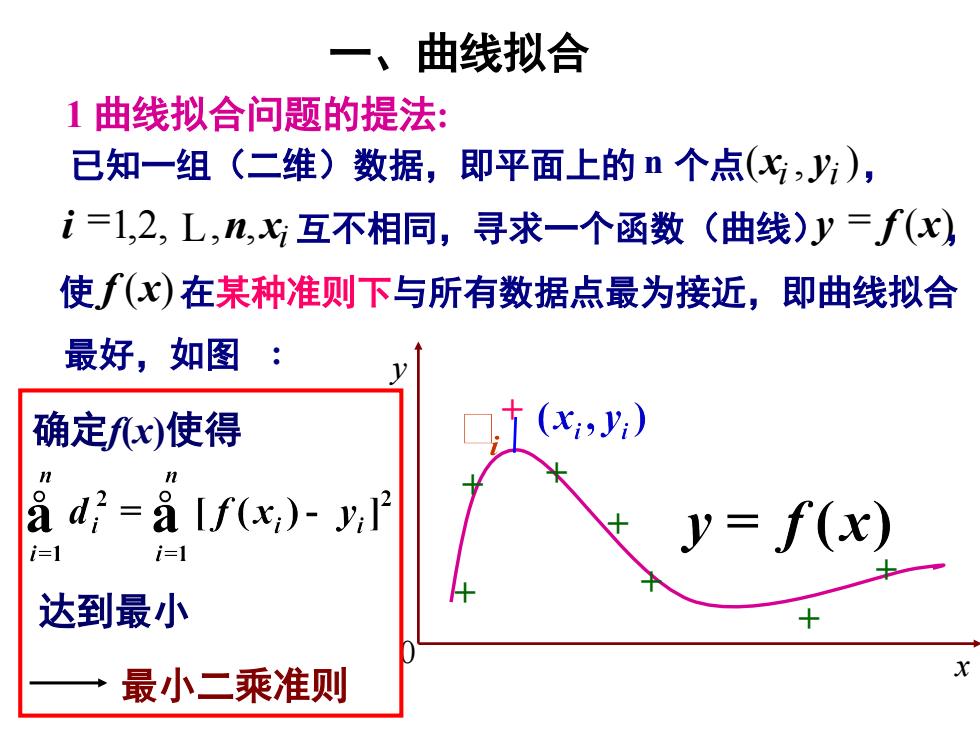
1 曲线拟合问题的提法: 已知一组(二维)数据,即平面上的 n 个点( , ) i i x y , n xi i =1,2, L, , 互不相同,寻求一个函数(曲线)y = f (x), 使 f (x)在某种准则下与所有数据点最为接近,即曲线拟合 最好,如图 : x y 0 + + + + + + + + 一、曲线拟合 确定f(x)使得 达到最小 最小二乘准则

2.用什么样的曲线拟合已知数据?(1)画图观察y+(x,,y,)(2)理论分析常用的曲线函数系类型:y= f(x)直线:y=ax+az+0x多项式:y=a,x" +L +amx+am+1a双曲线(一支):+a2y=xy =a,e"2x指数曲线:
2. 用什么样的曲线拟合已知数据? 常用的曲线函数系类型: (1)画图观察 (2)理论分析 指数曲线: 双曲线(一支): 多项式: 直线: x y 0 + + + + + + + +

3拟合函数中参数的确定以f(x)=a,x+a,为例,即确定a,a,使得J(aia?[ax,az,达到最小。ioi得到关为此,只需利用极值的必要条件10(k 1,2)2[a,x,a,)y,Ix,0a1,a2n2[a,x,a,y,]0il
3 拟合函数中参数的确定

二、人口预测的线性模型对于开始提出的实验问题,代如数据,计算得a, =15,a, =- 27754从而得到人口数与年份的函数关系为y = 15x - 27754线性预测模型把x=1999代如,估算出1999年的人口数为J=1252.1(百万)=12.52亿1999年实际人口数量为12.6亿
二、人口预测的线性模型 对于开始提出的实验问题, 代如数据,计算得 从而得到人口数与年份的函数关系为 把x=1999代如,估算出1999年的人口数为 y=1252.1(百万)=12.52亿 1999年实际人口数量为12.6亿。 线性预测模型

三、人口预测的Malthus模型英国人口学家Malthus根据百余年的人口统计资料,于1798年提出了著名的人口自然增长的指数增长模型。基本假设:人口(相对)增长率r是常数x(t)~时刻t 的人口,仁0时人口数为xdx= rx,P x(t)= xpertdt指数增长模型1 x(0) = xo实际中,常用 x(t)=ea+bt Inx(t)=α+bt
英国人口学家Malthus根据百余年的人口统计资 料,于1798年提出了著名的人口自然增长的指数增 长模型。 三、人口预测的Malthus模型 基本假设 : 人口(相对)增长率 r 是常数 x(t) ~时刻t 的人口, t=0时人口数为x0 指数增长模型 实际中,常用