
线性代数教程 第四章向量组的线性相关性 2346 3.向量的运算 向量的运算按照矩阵的运算规则进行。 第6顾
线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第6页 3.向量的运算 向量的运算按照矩阵的运算规则进行
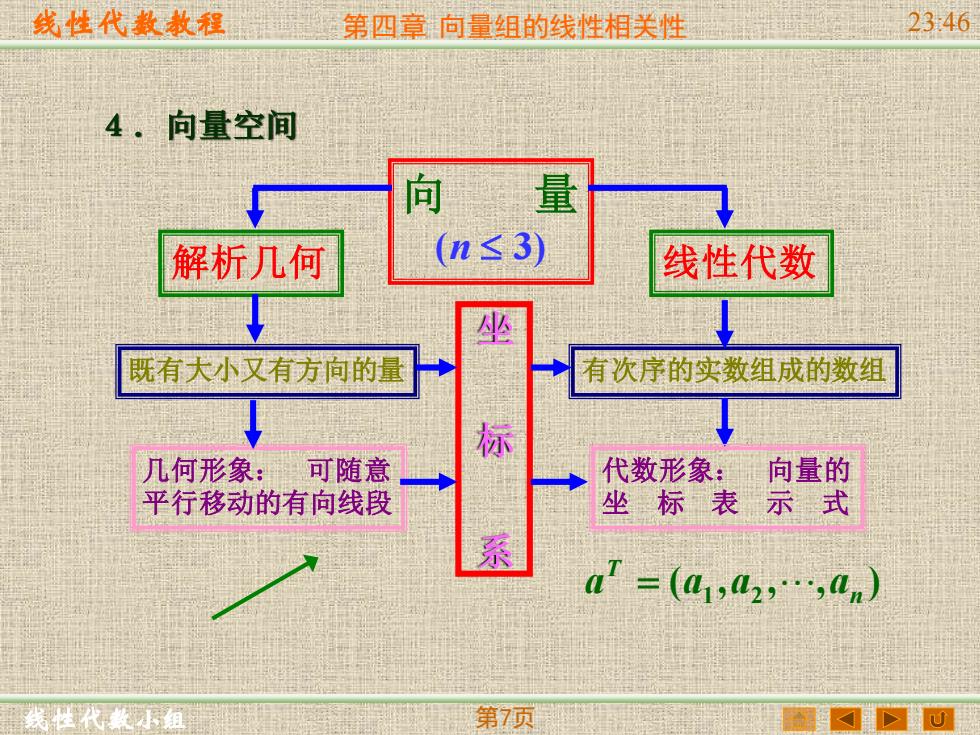
线性代教教程 第四章向量组的线性相送性 2346 4.向量空间 解析几何 (n≤3) 线性代数 坐 既有大小又有方向的量 有次序的实数组成的数组 标 几何形象:可随意 代数形象: 向量的 平行移动的有向线段 坐标表 示式 a=(a1,2,.,0n) 第7页
线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第7页 向 量 解析几何 (n 3) 线性代数 既有大小又有方向的量 有次序的实数组成的数组 几何形象: 可随意 平行移动的有向线段 代数形象: 向量的 坐 标 表 示 式 ( , , , ) 1 2 n T a = a a a 坐 标 系 4.向量空间
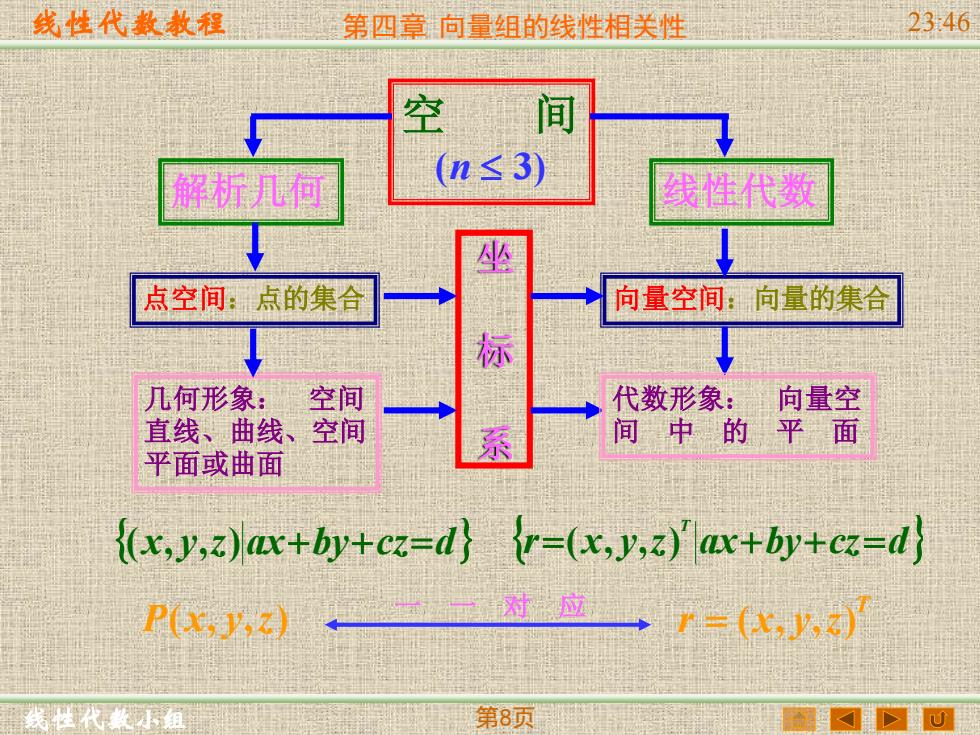
线性代数敖程 第四章向量组的线性相关性 23:46 间 解析几何 n≤3) 线性代数 坐 点空间:点的集合 向量空间:向量的集合 标 几何形象: 空间 代数形象: 向量空 直线、曲线、空间 平面或曲面 系 间中的平 面 {(x,y,z)ax+by+cz=d}r=(x,y,z)ax+by+cz=dj P) 一 对应一r=(X,山 第8项
线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第8页 空 间 (n 3) 解析几何 线性代数 点空间:点的集合 向量空间:向量的集合 坐 标 系 代数形象: 向量空 间 中 的 平 面 r x y z ax by cz d T =( , , ) + + = 几何形象: 空间 直线、曲线、空间 平面或曲面 (x, y,z)ax+by+cz=d P(x, y,z) r (x, y,z) T = 一 一 对 应

线性代教教程 第四章向量组的线性相送性 2346 n>3时,n维向量没有直观的几何形象 R==)R 叫做n维向量空间. ==)axta:x++ax.=b 叫做n维向量空间R"中的n-1维超平面. 第9页
线性代数教程 线性代数小组 第四章 向量组的线性相关性 23:46 第9页 R x x x xn x x xn R n T = =( 1 , 2 , , ) 1 , 2 , , x x x xn a x a x an xn b T = =( 1 , 2 , , ) 1 1+ 2 2++ = 叫做 n 维向量空间. n 3 时, n 维向量没有直观的几何形象. 叫做 维向量空间 R 中的 维超平面. n n n − 1