
利用DFT分析信号频谱、问题的提出一、、四种信号频谱之间的关系1三、利用DFT分析连续非周期信号频谱四、混叠现象、泄漏现象、栅栏现象五、DFT参数选取六、工程实际应用
利用DFT分析信号频谱 ◼ 一、问题的提出 ◼ 二、四种信号频谱之间的关系 ◼ 三、利用DFT分析连续非周期信号频谱 ◼ 四、混叠现象、泄漏现象、栅栏现象 ◼ 五、DFT参数选取 ◼ 六、工程实际应用

问题提出:如何利用数字方法分析信号的频谱?x(t) → X(jの) = (~ x(t)e-jatdtXr (t)e-jno' dtxr(t) → X(no)T+8x[k]e-jk?x[k] → X(ej?) =Mk=-802元N-1mkNx[k] → X[m] =x[k]ek=0
问题提出: 如何利用数字方法分析信号的频谱? + − − x t → X = x t e d t t j ( ) (j ) ( ) − → = T n t T xT t e d t T x t X n 0 j 0 ( ) 1 ( ) ( ) + =− − → = k k x k X e x k e j j [ ] ( ) [ ] − = − → = 1 0 2 j [ ] ~ [ ] ~ [ ] ~ N k mk N x k X m x k e
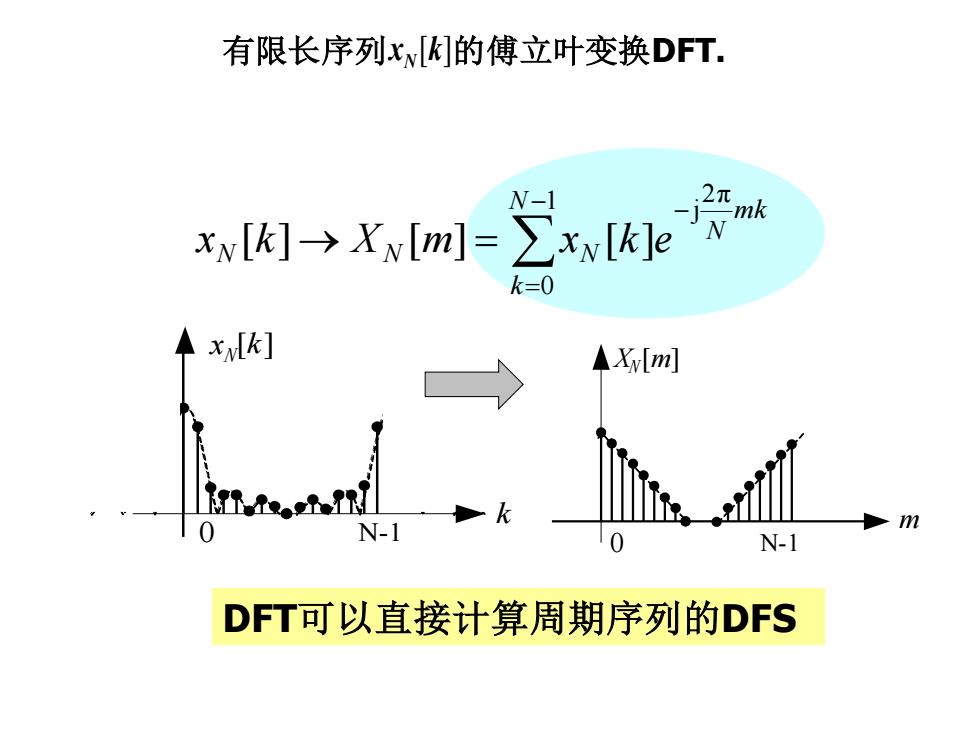
有限长序列xlk的傅立叶变换DFT2元N-1mkNx~[k] -→X~[m] = ZXv[klek=0x[k]AXi[m]KmN-100N-1DFT可以直接计算周期序列的DFS
有限长序列 xN [k] 的傅立叶变换DFT. − = − → = 1 0 2π j [ ] [ ] [ ] N k mk N N N N x k X m x k e 0 x [k] k N-1 N m X [m] 0 N-1 N DFT可以直接计算周期序列的DFS
可否利用DFT分析以上四种信号的频谱?基本原理利用信号傅立叶变换具有的信号时域与频域之间的对应关系,建立信号的DFT与四种信号频谱之间的关系。频域周期化时域的离散化一时域的周期化频域离散化
可否利用DFT分析以上四种信号的频谱? 基本原理 利用信号傅立叶变换具有的信号时域与频域 之间的对应关系,建立信号的DFT与四种信号频 谱之间的关系。 时域的离散化 时域的周期化 频域周期化 频域离散化
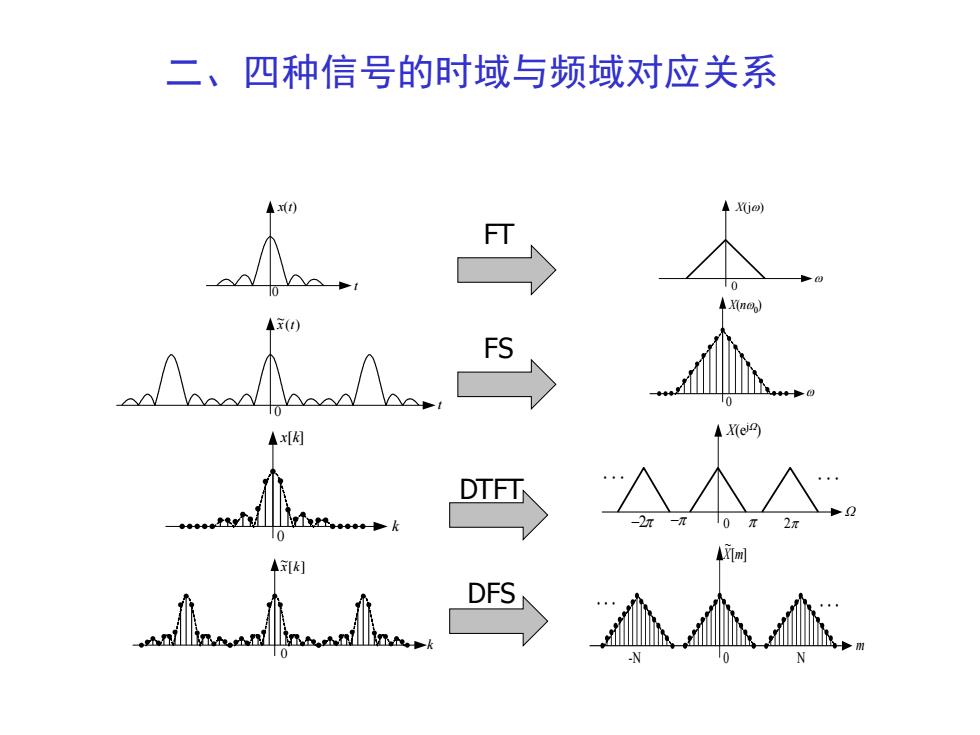
二、四种信号的时域与频域对应关系A(t)4 X(jo)ETX(no)4(0)FS4X(ej)Ax[K]DTFT5元102元2元元10AimlA[K]DFS4ak1oN-N
t x(t) 0 X(j) 0 t 0 ( ) ~x t k x[k] 0 0 [ ] ~x k k 二、四种信号的时域与频域对应关系 X(ej ) 0 . . −2 − 2 m [ ] ~ X m -N 0 N . . X(n0 ) 0 FT FS DTFT DFS