二、求解微分方程的一般思路与方法改写、探索解题思路的过程是一个不断比对、组合中间结果的“搭积木”的过程一阶可分离变量、齐次,一阶线性、伯努利,全微分微分方程可降阶三类可降阶欧拉方程高阶线性变系数齐次线性常系数非齐次线性
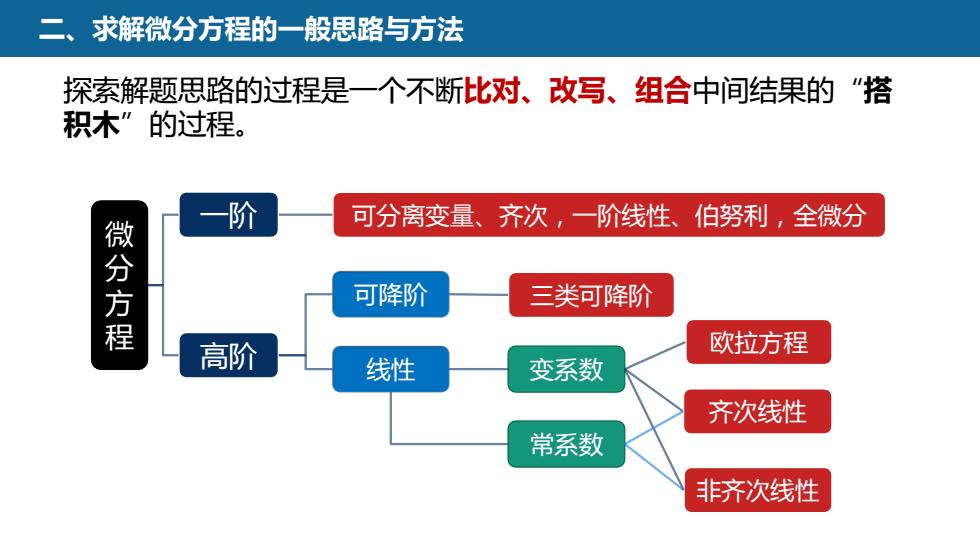
二、求解微分方程的一般思路与方法 探索解题思路的过程是一个不断比对、改写、组合中间结果的“搭 积木”的过程。 微 分 方 程 一阶 高阶 可分离变量、齐次,一阶线性、伯努利,全微分 可降阶 线性 三类可降阶 变系数 常系数 齐次线性 非齐次线性 欧拉方程

求解微分方程的一般思路与方法M (x)dx = N ()dy P 0 M (x)dx = 0 N (v)dy可分离变量微分方程dydudy=f(x)= j齐次微分方程uu+xexodxdxd.rye+P(W=Q()一阶线性微分方程0o0(x)e 0 P(c)dxy=eoP(x)dxadx +P0+P(=Q("(n0,1)伯努利方程du= (l- n)" dyu=I-nDdrdP(x,y)Q(x,)Pdx+Q(xdy=0全微分方程93qx1Q(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(uo)du+10D.0FO0YO
二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程

求解微分方程的一般思路与方法Mdx=NdyPOM()dx=ON()d)可分离变量微分方程Odudydyy= f (x,y)=uD齐次微分方程u+xExdxdxdxxye+P(W=Q()一阶线性微分方程0=eoP(r)dxao0(r/e0 P()dxdx+P0+P(=Q("(n0,1)伯努利方程du= (l- n)" dyu=I-nDdrdP(x,y)Q(x,)Pdx+Q(xdy=0全微分方程93qx1Q(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(uo)du+10D.0OVO
二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程

二、求解微分方程的一般思路与方法Mdx=NdyPOM()dx=ON(d)可分离变量微分方程dydudy1f(x)齐次微分方程Suu+xexodxdxd.rye+ P(x)y = Q(x)一阶线性微分方程0P y=e oP(x)dxgo0(re oPa)dxdx +福-0+P(x=Q("(n0,1)伯努利方程du= (l- n)n dyu=I-nddrP(x,y)Q(x,)P(rdx+Q(x)dy=0,全微分方程93qxXQ(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(u,yo)du+0D.0FO/YO
二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程

二、求解微分方程的一般思路与方法Mdx=NdyPOM()dx=ON(d)可分离变量微分方程Pdydudy1f(x)=齐次微分方程uu+xExOdxdxdrye+P(W=Q()一阶线性微分方程0o0(x)e 0 P(c)dxy=eoP(r)dxadx +D0e+ P(x)y = Q(x)y" (n 1 0, 1)伯努利方程du(- n)"dyyl-nsM二dxdxP(x,y)Q(x,)P(rdx+Q(x)dy=0全微分方程qyqx1Q(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(uJo)du+0D.0FO0YO
二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程