《线性代数》课程教学资源（课件讲稿，B）第四章特征值与特征向量_4-2矩阵的相似对角化

二.矩阵的相似对角化(2)定理222则，，,是A的全部特征值.设矩阵A～△=2a-a-=(a-a)(a-z)...(a-a.)证：[al-a-a.的全部特征值是：，，…，nA与Λ的特征值相同A的全部特征值是：，，，,加油！

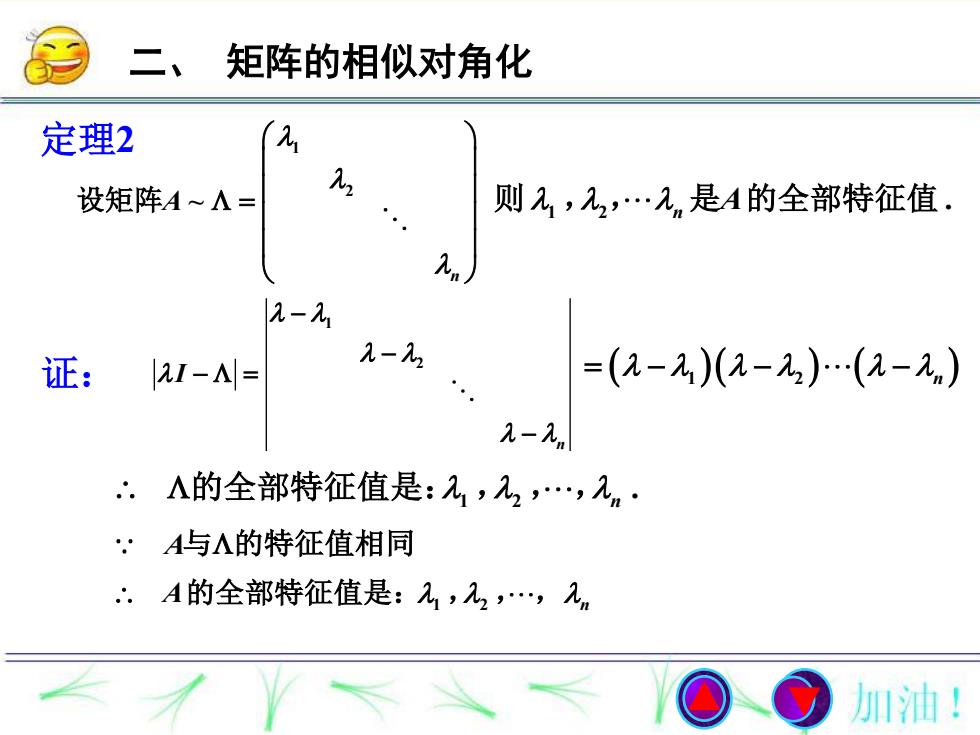
二、 矩阵的相似对角化 1 2 ~ n A                  设矩阵 1 2 . 则    ， ， n 是A的全部特征值 定理2 1 2 .  的全部特征值是：   ， ， ，n  A的全部特征值是：   1 2 ， ， ， n           1 2    n  A与的特征值相同 1 2 n I              证：

定理3n阶矩阵A与对角矩阵相似的充分必要条件是A有n个线性无关的特征向量证：充分性　讠设A有n个线性无关的特征向量：P，Pz，,P,Ap, = 2,P, (i=1,2,.*,n)a2令 P=(P, P2, ... ,PnA=则 AP=P△P-1AP= △2A~A=加油！

充分性 设A n 有 个线性无关的特征向量： 定理3 n阶矩阵A与对角矩阵相似的充分必要条件 是A有n个线性无关的特征向量. 1 2 , , , n p p p 1 2 n                  1 2 ~ n A                    1,2, ,  Ap p i n i i i    令 P p p p   1 2 , , , n  1 AP P P AP  则     证：

元2,必要性设P-IAP=Λ=则 AP=P△2令 P=(P，P2，...,Pn(Ap Ap2... Apn)=(αiP 22P2... 2nAp, = 2;P, (i = 1,2,..,n)Pi，P2，Pn是A的n个线性无关的特征向量加油！

 Ap Ap Ap p p p 1 2 1 1 2 2 n n n        1 1 2 n P AP                    必要性 设 则 AP P   令 P p p p   1 2 , , , n   1,2, ,  Ap p i n i i i    1 2 , , , n p p p 是A n 的 个线性无关的特征向量

3-1求A100例若A=a-12-31解：A的特征多项式为|aI-A(2-2)(2-4)2-3→A的特征值为,=2，=4对 = 2,2-3x,(2I - A)x =2-3X加油！

1 2    A的特征值为  2, 4 解：A的特征多项式为 100 3 1 1 3 A A          例 若 ，求 3 1 1 3 I A           ( 2)( 4)   1 2 1 1 1 1 x x               1 2 2 3 1 (2 ) 1 2 3 x I A x x                2, 对1 