
导航 2.填空:(1)全集 在研究集合与集合之间的关系时,如果所要研究的集合都是 的子集,那么称这个 为全集,通常用 符号表示
导航 2.填空:(1)全集 在研究集合与集合之间的关系时,如果所要研究的集合都是 某一给定集合的子集,那么称这个给定的集合为全集,通常用 符号 U 表示
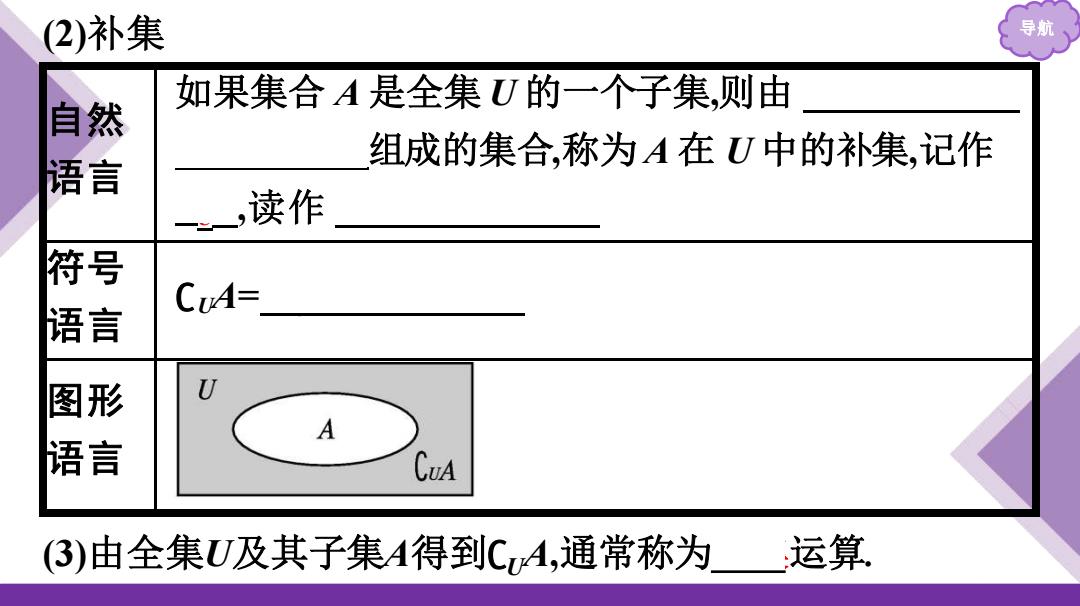
(2)补集 导航 如果集合A是全集U的一个子集,则由 房 组成的集合,称为A在U中的补集,记作 言 ,读作 符语 号 CuA= 图形 U 语言 A CuA (3)由全集U及其子集A得到CA,通常称为运算
导航 (2)补集 自 然 语 言 如果集合 A 是全集 U 的一个子集,则由 U 中不属于 A 的所有元素组成的集合,称为 A 在 U 中的补集,记作 ∁U A,读 作 A 在 U 中的补集 符 号 语 言 ∁U A={x|x∈U,且 x∉A} 图 形 语 言 (3)由全集U及其子集A得到∁UA,通常称为补集运算

导航 3.补集运算的结果是数还是集合? 提示:集合 4.做一做:已知U={0,1,2,3,4},A={0,4},B={2,3,4},求CA,CB, AUB,CIAUB). 解:CA={1,2,3},CB={0,1},AUB={0,2,3,4},CAUB)={1
导航 3.补集运算的结果是数还是集合? 提示:集合. 4.做一做:已知U={0,1,2,3,4},A={0,4},B={2,3,4},求∁UA,∁UB, A∪B,∁U(A∪B). 解:∁UA={1,2,3},∁UB={0,1},A∪B={0,2,3,4},∁U(A∪B)={1}

导 二、补集的性质 【问题思考】 1.已知U={1,2,3,4,5,6},A={1,2,3},B={2,3,4},求 AUB,A∩B,CA,CB,AU(CA),A∩(CA),C(CA),(CA)∩(CvB) (CA)U(CuB),Cu(AnB),CU(AUB). 提示:AUB={1,2,3,4},A∩B={2,3},CA={4,5,6},CB={1,5,6, AU(CUA)=U,A0(CUA)=,CU(CA)=A,(CA)(CUB)=15,6, (CA)U(CB)={1,4,5,6},CA∩B)={1,4,5,6},CAUB)={5,6
导航 二、补集的性质 【问题思考】 1.已知U={1,2,3,4,5,6},A={1,2,3},B={2,3,4},求 A∪B,A∩B,∁UA,∁UB,A∪(∁UA),A∩(∁UA),∁U(∁UA),(∁UA)∩(∁UB), (∁UA)∪(∁UB),∁U(A∩B),∁U(A∪B). 提示:A∪B={1,2,3,4},A∩B={2,3},∁UA={4,5,6},∁UB={1,5,6}, A∪(∁UA)=U,A∩(∁UA)=⌀,∁U(∁UA)=A,(∁UA)∩(∁UB)={5,6}, (∁UA)∪(∁UB)={1,4,5,6},∁U(A∩B)={1,4,5,6},∁U(A∪B)={5,6}

导航 2.填空:补集的性质 ()AU(CA)=-,A∩(CA)=-,C(CA)=_· (2)(CA)∩(CB)= ,(CuA)U(CuB)= 3.做一做:设全集为U,A={1,2,4,5},CA={3},则U等于( A.0 B.{1,2,4,5} C.{1,2,3,4,5}D.{3} 答案:C
导航 2.填空:补集的性质 (1)A∪(∁UA)= U ,A∩(∁UA)= ⌀ ,∁U(∁UA)= A . (2)(∁UA)∩(∁UB)= ∁U(A∪B) ,(∁UA)∪(∁UB)= ∁U(A∩B) . 3.做一做:设全集为U,A={1,2,4,5},∁UA={3},则U等于( ) A.⌀ B.{1,2,4,5} C.{1,2,3,4,5} D.{3} 答案:C