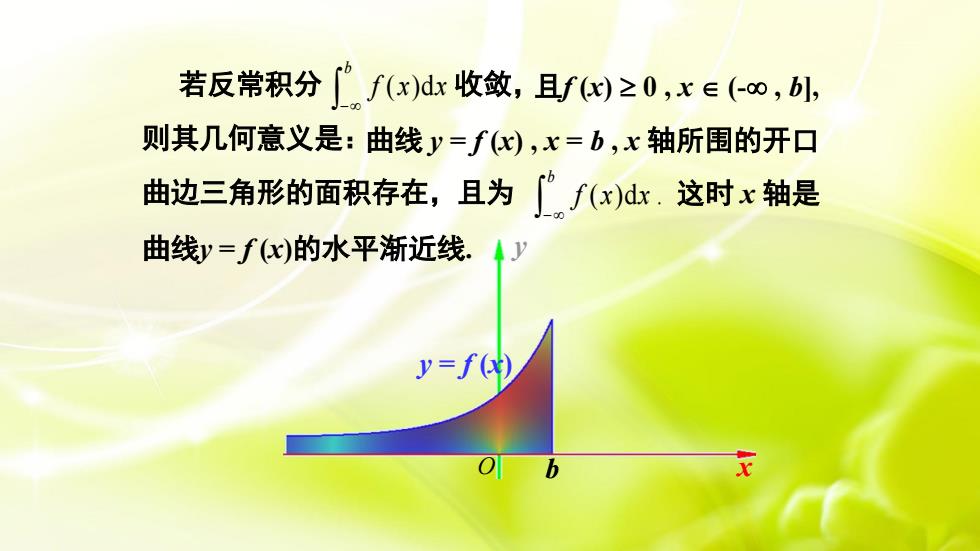
若反常积分[f(x)dx 收敛, 且f (x)≥0 ,x E (-o0 , bl,则其几何意义是:曲线y=f(x),x=b,x轴所围的开口曲边三角形的面积存在,且为f(x)dx.这时x轴是曲线y=f(x)的水平渐近线y=f()xOb
若反常积分 − b f (x)dx 收敛, 则其几何意义是: 曲边三角形的面积存在,且为 ( )d . − b f x x 曲线y = f (x)的水平渐近线. 且f (x) 0 , x (- , b], 曲线 y = f (x) , x = b , x 轴所围的开口 b x y y = f (x) O 这时 x 轴是
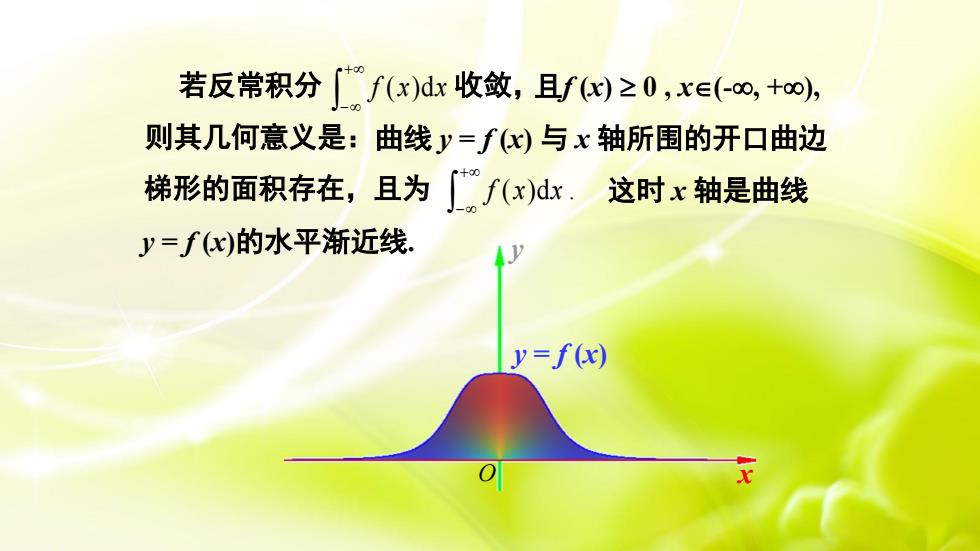
若反常积分[f (x)dx 收敛, 且f(x) ≥ 0 ,xe(-00, +o0),则其几何意义是:曲线=f(x)与x轴所围的开口曲边梯形的面积存在,且为f(x)dx.这时x轴是曲线y=f(x)的水平渐近线y=f(x)O
若反常积分 + − f (x)dx 收敛, 则其几何意义是: 梯形的面积存在,且为 ( )d . + − f x x y = f (x)的水平渐近线. 且f (x) 0 , x(-, +), 曲线 y = f (x) 与 x 轴所围的开口曲边 x y y = f (x) O 这时 x 轴是曲线

dx*+00例1计算反常积分1+x20dxdxdxco+8+00解十1+x2Jo1+-00yYOV=limdx + limdx1+x222b-→+Jo1 +xJa1+xa→-00= lim [arctan x], + lim [arctan x]§0-8b=(-)+=-lim arctana + lim arctanb=元.b-→+00a→-00
例1 计算反常积分 . 1 2 + − + x dx 解 + − + 2 1 x dx − + = 0 2 1 x dx + + + 0 2 1 x dx + = →− 0 2 1 1 lim a a dx x + + →+ b b dx x 0 2 1 1 lim 0 lim arctan a a x →− = 0 lim arctan b b x →+ + a a lim arctan →− = − b b lim arctan →+ + . 2 2 = + = − x o y 2 1 1 y x = +

若F(αx)是f(x)的原函数引入记号F(+o0)= lim F(x); F(-0)= lim F(x)X→-00→+8则有类似牛一莱公式的计算表达式:+8= F(+oo)-F(a)[+° f(x)dx = F(x)b[ f(x)dx= F(x)= F(b)- F(-80)-8+8[~ (x)dx = F(x)= F(+)-F(-8)-8
若F x f x ( ) ( ) , 是 的原函数 引入记号 ( ) lim ( ) ; x F F x → + + = ( ) lim ( ) x F F x → − − = 则有类似牛 – 莱公式的计算表达式 : ( )d a f x x + = F x( ) a + = + − F F a ( ) ( ) ( )d b f x x − b − = − − F b F ( ) ( ) f x x ( )d + − + − = + − − F F ( ) ( ) = F x( ) = F x( )

例2证明反常积分dx当p>1时收敛,4当p≤1时发散.(第一类p积分)证 (1) p= 1,** dx= _dx =[In x]°= +,[+80, p<1@ [高(高因此当p>1时反常积分收敛,其值为p-ii当p≤1时反常积分发散
证 (1) p = 1, + 1 1 dx x p + = 1 1 dx x + = 1 ln x = +, (2) p 1, + 1 1 dx x p + − − = 1 1 1 p x p − + = , 1 1 1 , 1 p p p 因此当 p 1时反常积分收敛,其值为 1 1 p − ; 当 p 1时反常积分发散. 1 1 2 1 1 ( ) p dx p x p p + 例 证明反常积分 当 时收敛, 当 时发散.第一类 积分