
性质6设M及m分别是函数 f(x)在区间[a,b1上的最大值及最小值, 则m(b-a)≤'f(x)r≤M(b-a). 证:m≤f(x)≤M, ·mdc≤f(x)adc≤Md, m(b-a)≤f(x≤Mb-a). (此性质说明,由被积函数在积分区间上的 最值,可用于估计积分值的大致范围) 2012329 素山医学院信息工程学院高等数学教研室

性质7(定积分中值定理) 如果函数f(x)在闭区间a,b上连续, 则在积分区间[a,b]上至少存在一个点5, 使f(x)=f(5)b-a).(a≤5≤b) 积分中值公式 证:m(b-a)≤f(x≤Mb-a) m≤ 由闭区间上连续函数的介值定理知 2012329 素山医学院信息工程学院高等数学教研常
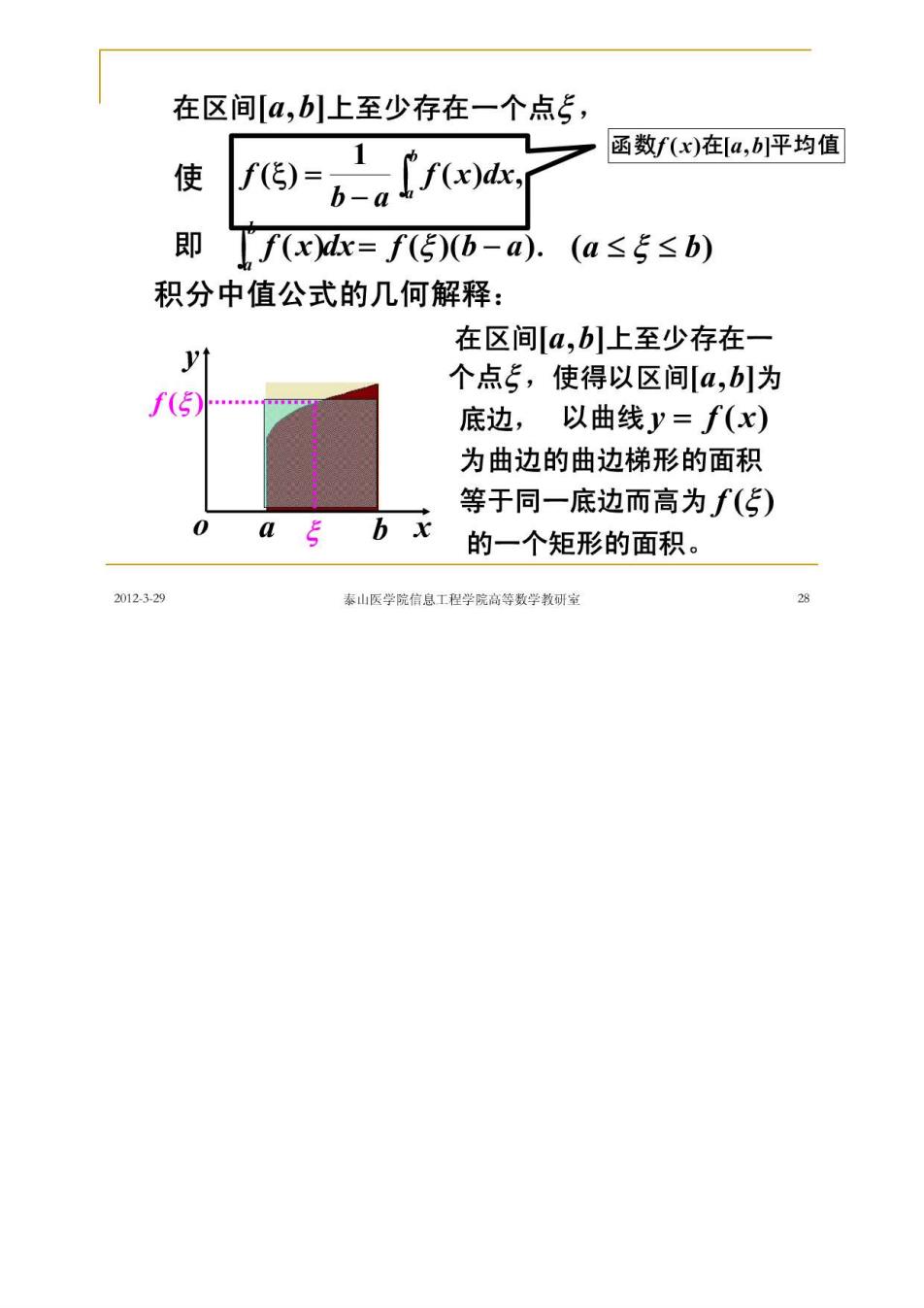
在区间[a,b]上至少存在一个点5, 函数f(x)在a,b小平均值 使 f5)= 即 f(xx=f(5)(b-a).(a≤5≤b) 积分中值公式的几何解释: 少 在区间a,b1上至少存在一 个点5,使得以区间a,b]为 f() 底边, 以曲线y=f(x) 为曲边的曲边梯形的面积 等于同一底边而高为f(5) 0 a 的一个矩形的面积。 2012329 奉山医学院信息工程学院高等数学教研室

例2比较积分值e*d和∫xdr的大小 解 令f(x)=e*,g(x)=xx∈【-2,01 f(x)>0,g(x)<0.f(x)>g(x) 于是由性质5的推论1edk<dc. 2012329 奉山医学院信息工程学院高等数学教研案
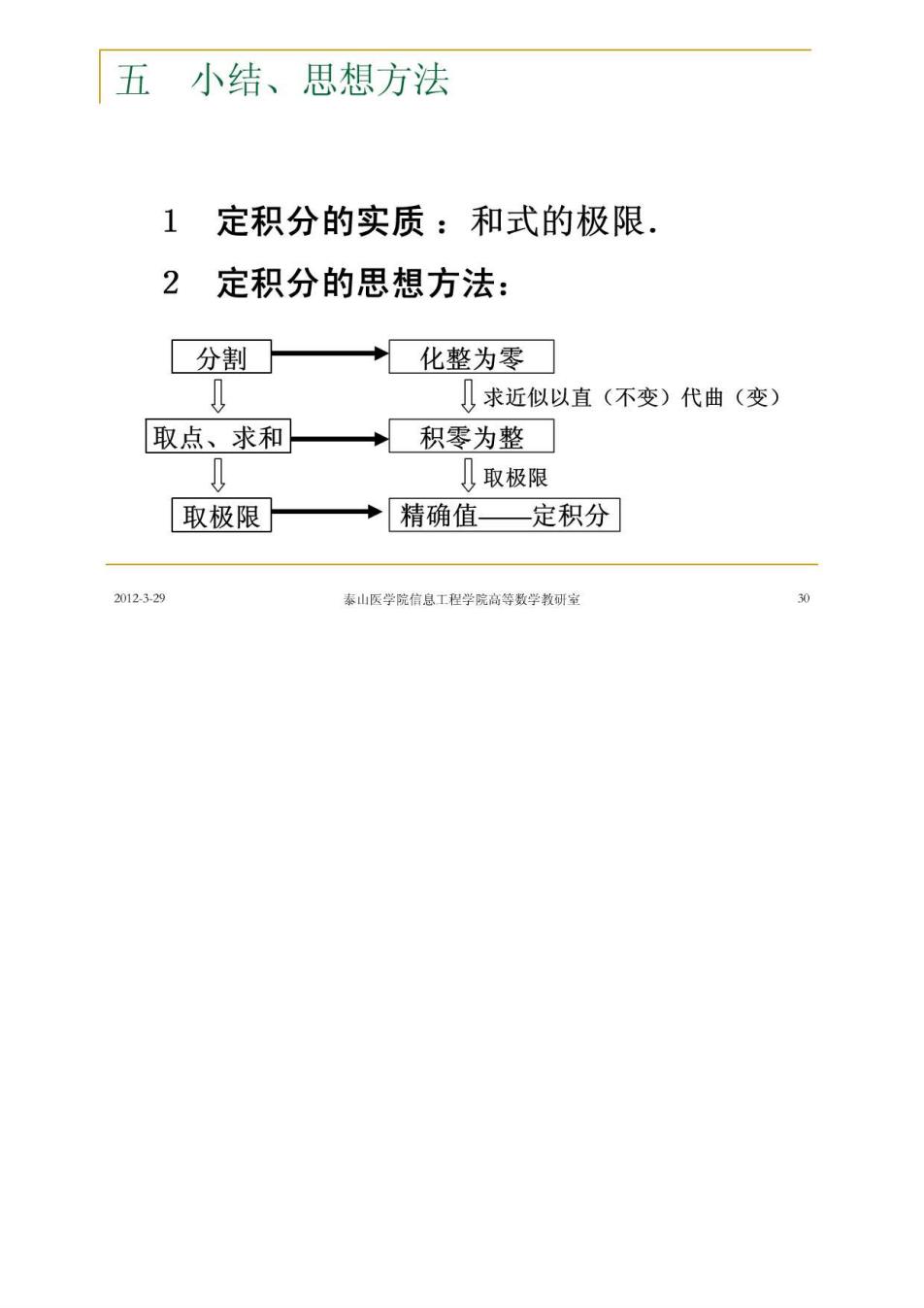
五小结、思想方法 1定积分的实质:和式的极限. 2定积分的思想方法: 分割☐ 化整为零 ↓求近似以直(不变)代曲(变) 取点、求和→积零为整☐ ↓取极限 取极限 →精确值一定积分 2012329 素山医学院信息工程学院高等数学教研室