(3)能量关系 电容不断释放能量被电阻吸收, 直到全部消耗完毕 设uc(0)=Uo 电容放出能量: 1-2 电阻吸收(消耗) 能量: W=R-eR咖 21 2t R R
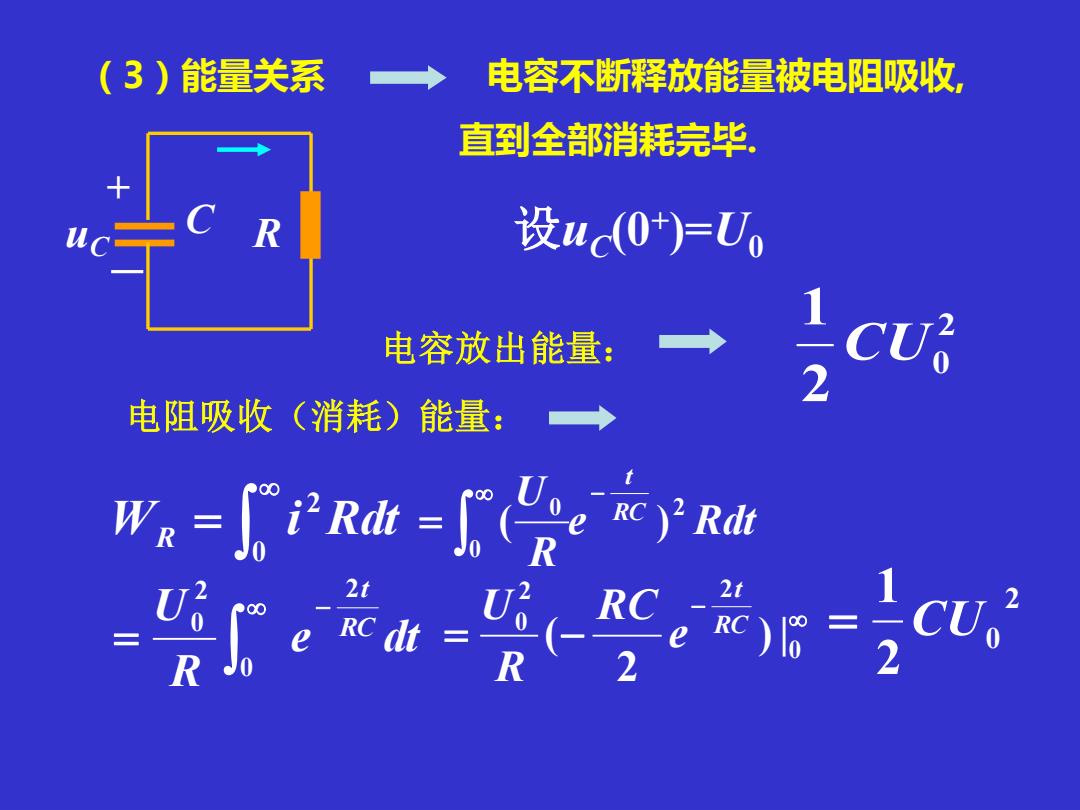
(3)能量关系 W i Rdt R = 0 2 电容不断释放能量被电阻吸收, 直到全部消耗完毕. 设uC (0+ )=U0 电容放出能量: 2 0 2 1 CU 电阻吸收(消耗)能量: e Rdt R U RC t 2 0 0 ( ) − = 2 0 2 1 = CU uC R + - C e dt R U RC 2t 0 2 0 − = − = − 0 2 2 0 )| 2 ( RC t e RC R U
例 已知图示电路中的电容原本充有24V电压,求K闭 合后,电容电压和各支路电流随时间变化的规律。 解 这是一个求一阶RC零输 入响应问题,有: 32 u.=Ue Rc t≥0 代入U,=24VT=RC=5×4=20s 等效电路 t>0 4。=24e20/ t≥0 i,=4c/4=6e20A 分流得:4-子=北546==2克1
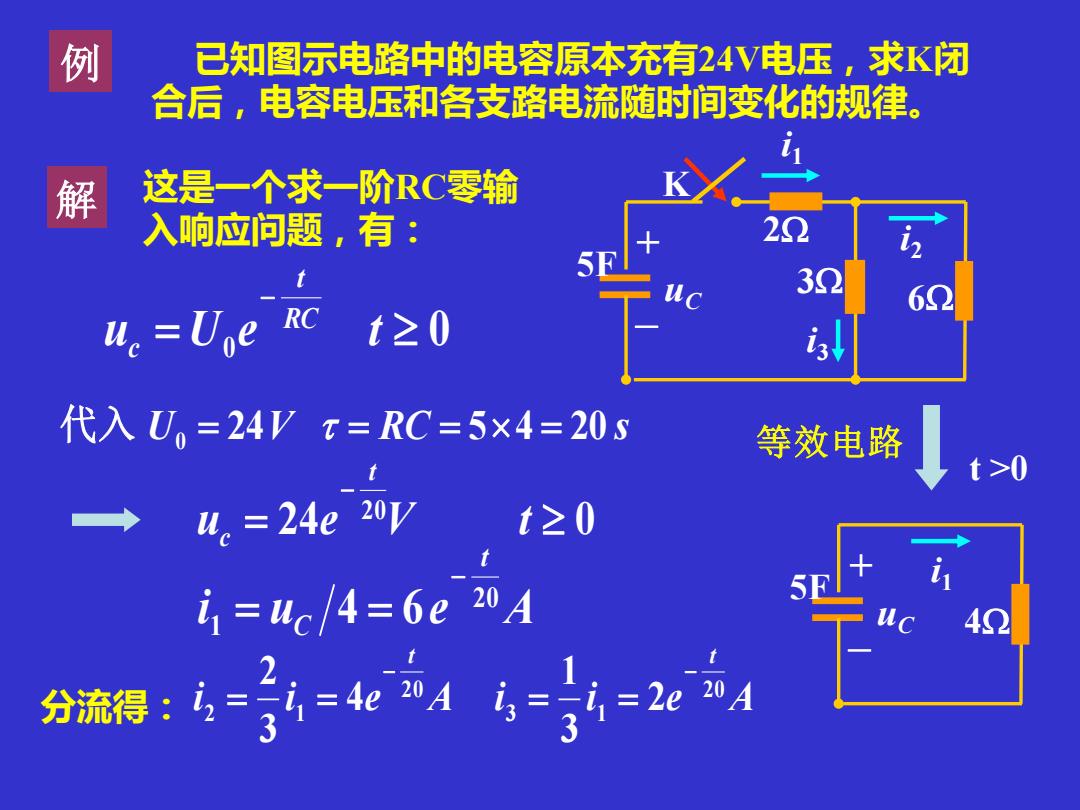
例 已知图示电路中的电容原本充有24V电压,求K闭 合后,电容电压和各支路电流随时间变化的规律。 解 这是一个求一阶RC零输 入响应问题,有: i3 K 3 + uC 2 6 5F - i2 i1 + uC 4 5F - i1 t >0 等效电路 0 = 0 − u U e t RC t c U 24V RC 5 4 20 s 代入 0 = = = = 24 0 20 = − u e V t t c 分流得: i u e A t C 20 1 4 6 − = = i i e A t 20 2 1 4 3 2 − = = i i e A t 20 3 1 2 3 1 − = =
2.RL电路的零输入响应 z(0*)=iz(0)= R K0) 3L di +Ri=0t≥0 dt t>0 R i(t)=Ae L3 代入初始值i0=1。 A=i0*)尸10 R 得i(t)=Ie”=Iez t≥0
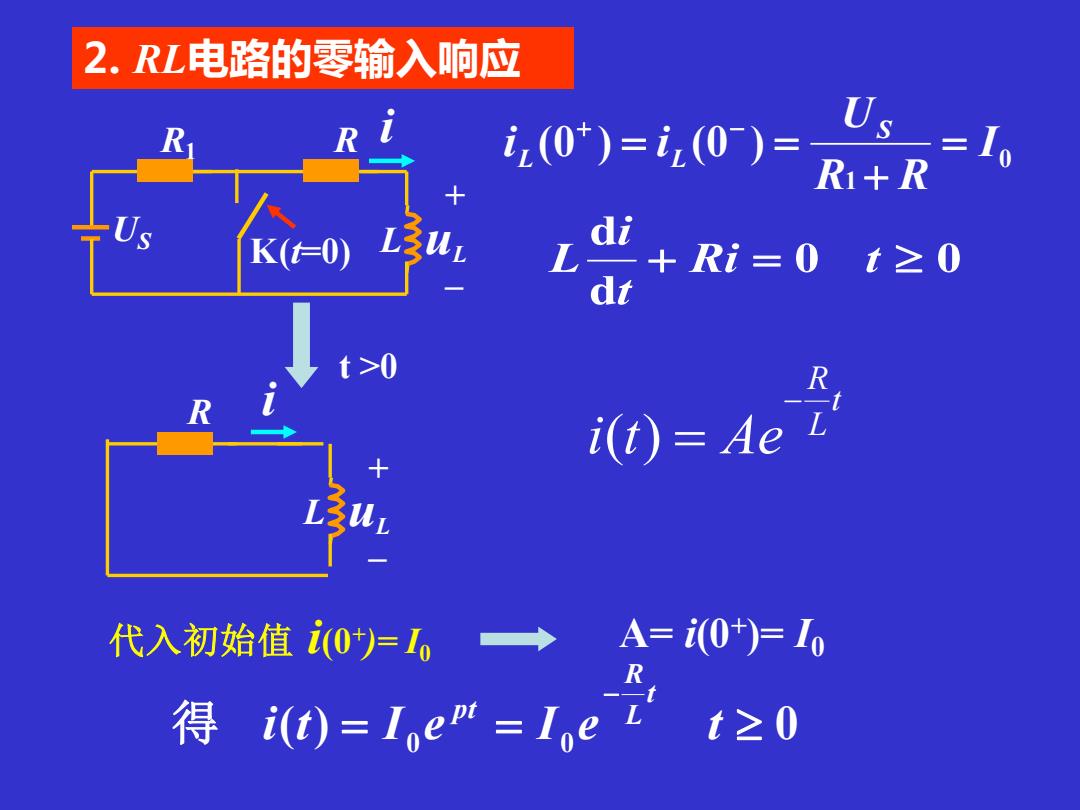
2. RL电路的零输入响应 代入初始值 i(0+ )= I0 A= i(0+ )= I0 0 1 (0 ) (0 ) I R R U i i S L L = + = = + − 0 0 d d + Ri = t t i L i K(t=0) US L + – uL R1 R t L R i t Ae − ( ) = ( ) 0 = 0 = 0 − i t I e I e t t L R 得 p t t >0 i L + – uL R
i(t)=Ie LIR t20一u,)=L=-R1,e t 从以上式子可以得出: (1)电压、电流是随时间按同一指数规律衰减的函数; ↑元 连续 函数 跃变 (2)响应与初始状态成线性关系,其衰减快慢与LR有关;
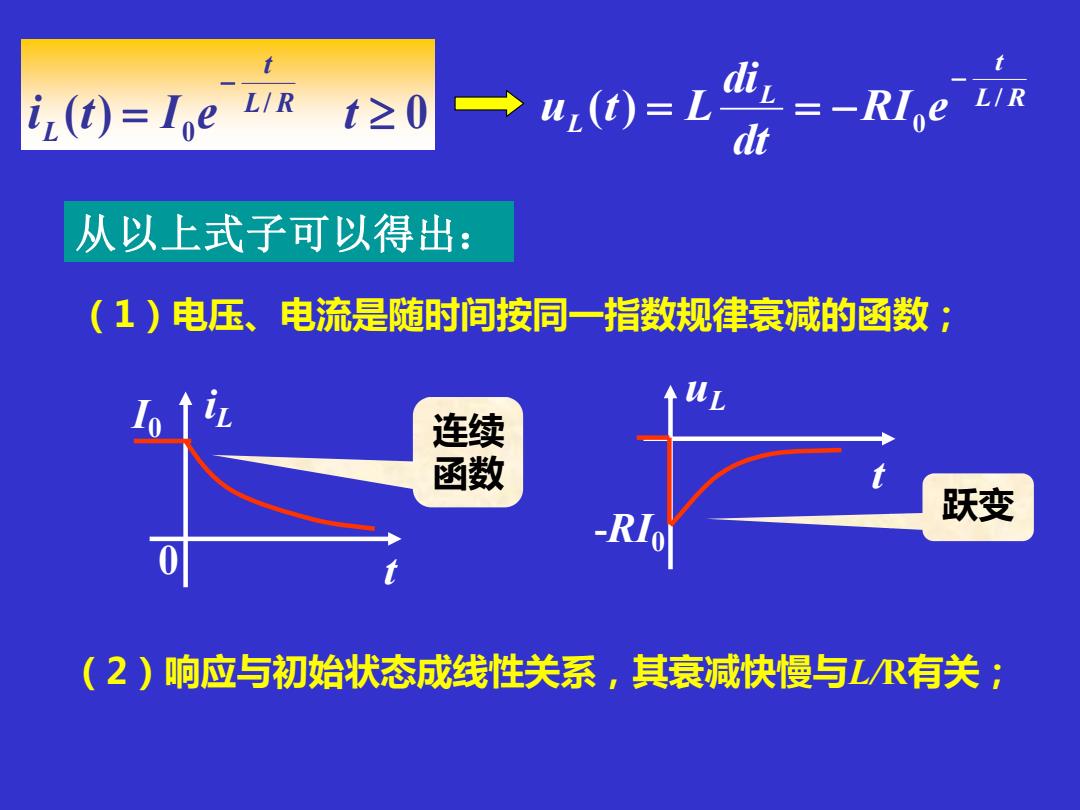
L R t L L RI e dt di u t L / 0 ( ) − ( ) / 0 = = − = 0 − i t I e t L R t L -RI0 uL t t I0 iL 0 从以上式子可以得出: 连续 函数 跃变 (1)电压、电流是随时间按同一指数规律衰减的函数; (2)响应与初始状态成线性关系,其衰减快慢与L/R有关;

令x=LR,称为一阶RL电路时间常数 1=会1=豪-1实胶=安欧1= 亨 韦 伏.秒 t=L/R 时间常数x的大小反映了电路过波过程时间的长短 x大→过渡过程时间长 ?小过渡过程时间短
令 = L/R , 称为一阶RL电路时间常数 [ ] [ ] [ ] [ ] [ ] [秒] 安 欧 伏 秒 安 欧 韦 欧 亨 = = = = = R L 大 → 过渡过程时间长 小 → 过渡过程时间短 时间常数 的大小反映了电路过渡过程时间的长短 = L/R