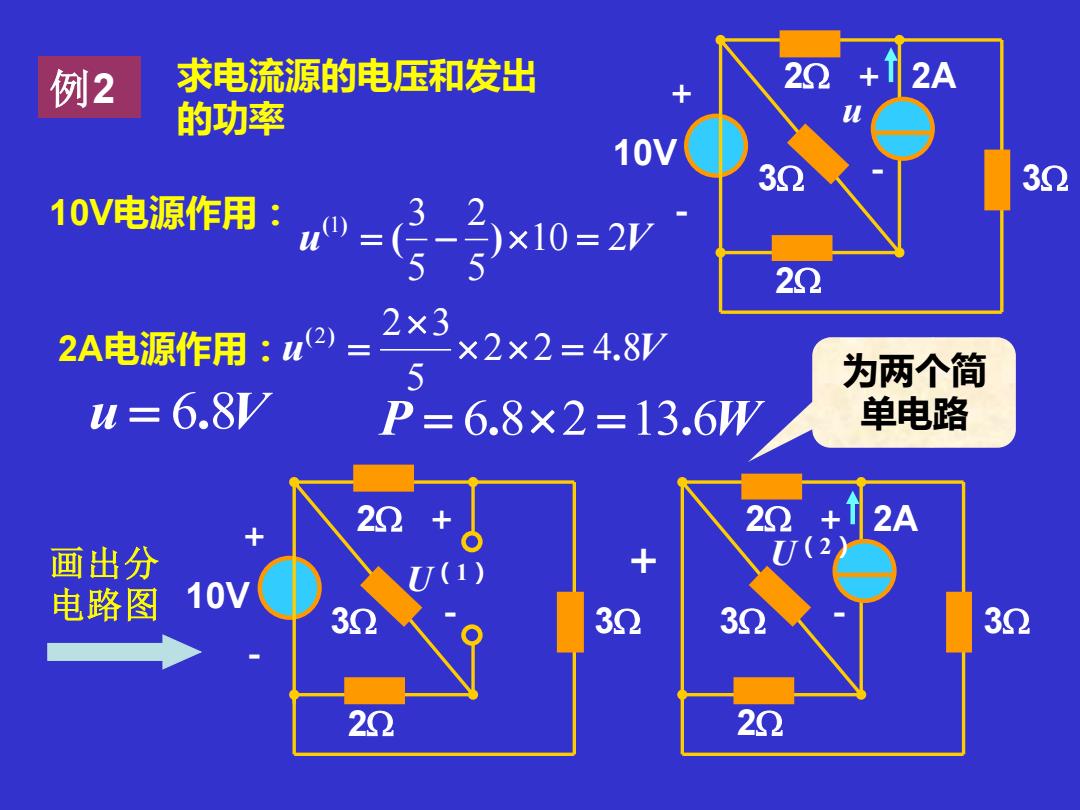
例2 求电流源的电压和发出 2 2+12A 的功率 10V 30 1oN电源作用:”=子x10=2y 20 2A电源作用:u2= 2×3 ×2×2=4.8/ 5 为两个简 u=6.8/ P=6.8×2=13.6WW 单电路 22 22+2A 画出分 电路图 10V 32 32 32 32 20 20
例2 + - 10V + 2A - u 2 3 3 求电流源的电压和发出 2 的功率 + - 10V + - U(1) 2 3 3 2 + 2A - U(2) 2 3 3 2 + u 10 2V 5 2 5 1 3 = ( − ) = ( ) u 2 2 4 8V 5 2 2 3 . ( ) = = u = 6.8V P = 6.82 =13.6W 画出分 电路图 为两个简 单电路 10V电源作用: 2A电源作用:
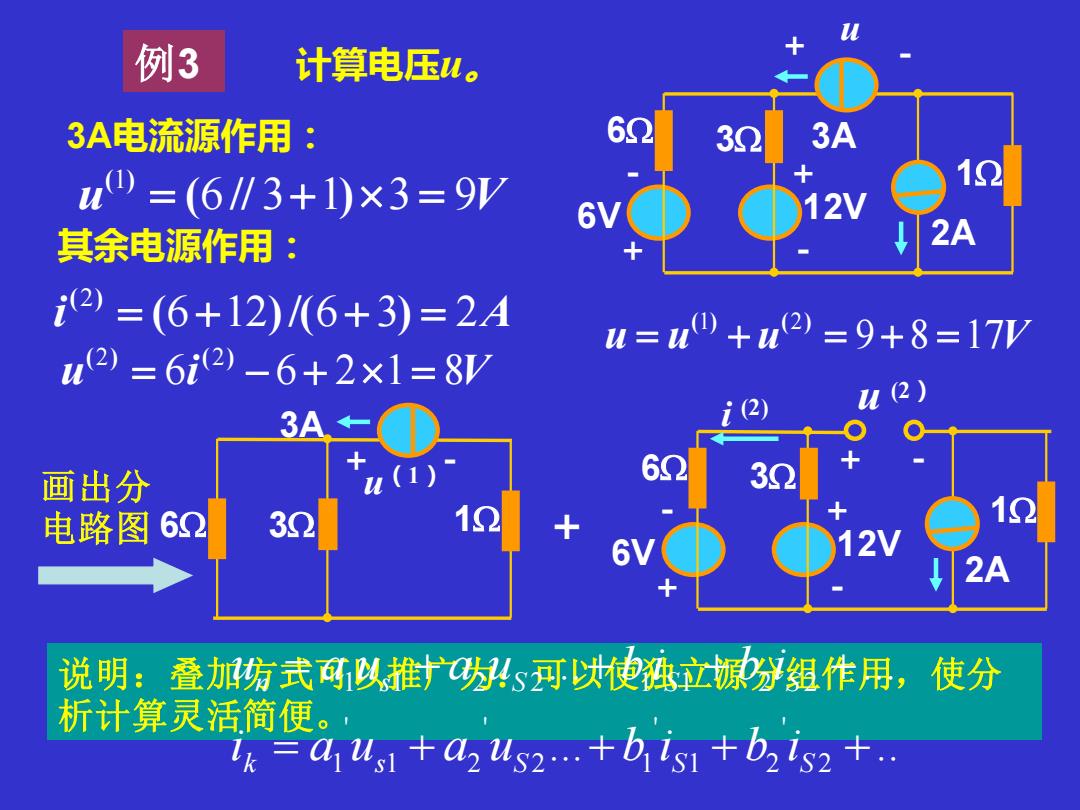
例3 计算电压4。 3A电流源作用: 60 32 3A u0=(61∥3+1)×3=9 12V 其余电源作用: 2A i2)=(6+12)/(6+3)=2A u=㎡0+u2)=9+8=17W u2=6i2)-6+2x1=8V 2) 3A (2) 画出分 (1) 32 电路图62 30 12V 2A 说明:叠加方式可以推广为!s可以使独立源分组作用,使分 析计算灵活简便。 7兰a1u1+a2us2…+bis1+b2is2+
例3 u + - 12V 2A + - 1 6 3 3A 6V 计算电压u。 + - 画出分 电路图 1 3A 6 3 + - u(1) + u 6 3 1 3 9V 1 = ( // + ) = ( ) u 6i 6 2 1 8V 2 2 = − + = ( ) ( ) + - 12V 2A + - 1 6 3 6V + - u (2) i (2) i 6 12 6 3 2A 2 = ( + )/( + ) = ( ) u u u 9 8 17V 1 2 = + = + = ( ) ( ) 说明:叠加方式可以推广为:可以使独立源分组作用,使分 析计算灵活简便。 3A电流源作用: 其余电源作用: ... .. ... ... 2 ' 1 2 ' 2 1 ' 1 2 ' 1 1 1 2 2 1 1 2 2 = + + + + = + + + + k s S S S n s S S S i a u a u b i b i u a u a u b i b i
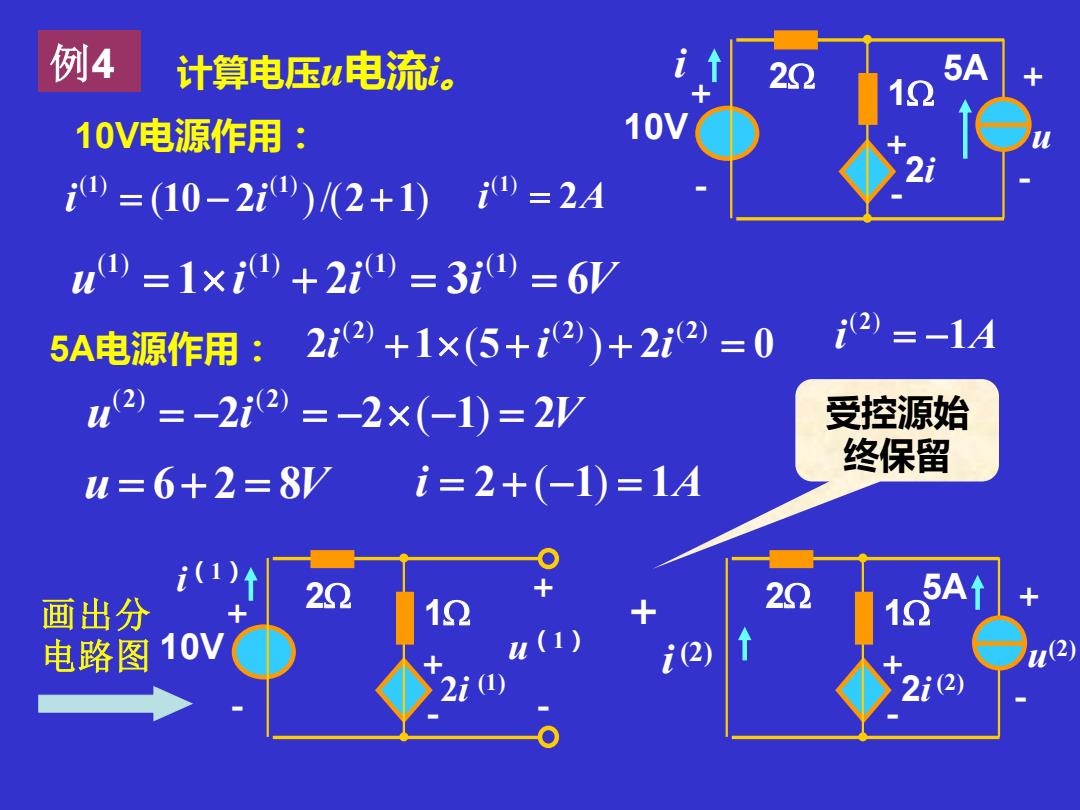
例4 计算电压u电流i。 5A 12 10V电源作用: 10V =(10-2i)(2+1) 0=2A n0=1×i0+2i0=3i0=6y 5A电源作用:2i2+1×(5+i2)+2i2)=0 i2=-1A n2=-2i2=-2×(-1)=2V 受控源始 终保留 u=6+2=8V i=2+(-1)=1A i(1) 画出分 22 12 20 5At 1 电路图 10V (1) i2) 2i2)
例4 计算电压u电流i。 画出分 电路图 u(1) + - 10V 2i + (1) - 1 2 + - i(1) + ( )/( ) ( ) ( ) 10 2 2 1 1 1 i = − i + u 1 i 2i 3i 6V 1 1 1 1 = + = = ( ) ( ) ( ) ( ) i 2A 1 = ( ) u = 6+ 2 = 8V u + - 10V 2i + - 1 i 2 + - 5A u (2) 2i + (2) - 1 i (2) 2 + - 5A ( ) ( ) ( ) ( ) 2 1 5 2 0 2 2 2 i + + i + i = i 1A 2 = − ( ) u 2i 2 1 2V 2 2 = − = − (− ) = ( ) ( ) i = 2 + (−1) = 1A 受控源始 终保留 10V电源作用: 5A电源作用:
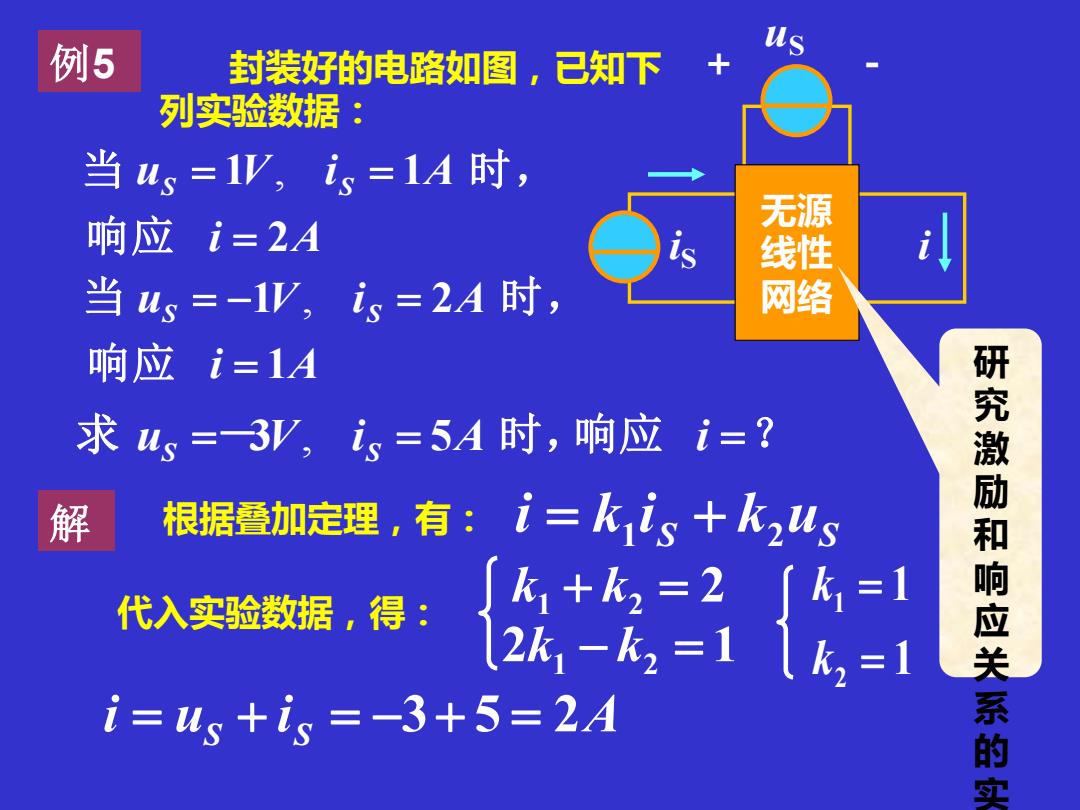
例5 us 封装好的电路如图,已知下 列实验数据: 当us=1V,is=1A时, 响应i=2A 无源 线性 当4s=-1,is=2A时, 网络 响应i=1A 求4s=3V,is=5A时,响应i=? 解 根据叠加定理,有:i=kis+k24s 代入实验数据,得: k+k2=2∫k=1 2k1-k2=11k2=1 i=4s+i、=-3+5=2A 研究激励和响应关系的实
例5 无源 线性 网络 uS i + - iS 封装好的电路如图,已知下 列实验数据: i A uS V i S A 2 1 1 = = = , 响 应 当 时 , i A uS V i S A 1 1 2 = = − = , 响 应 当 时 , 求 uS =-3V, i S = 5A 时, 响应 i =? 解 根据叠加定理,有: S k uS i k i = 1 + 2 代入实验数据,得: k1 + k2 = 2 2k1 − k2 = 1 1 1 2 1 = = k k i = uS + i S = −3+ 5 = 2A 研 究 激 励 和 响 应 关 系 的 实 验

齐性原理(homogeneity y property) 线性电路中,所有激独立源)都增大(或减小)同样 的倍数,则电路中响应(电压或电流)也增大(或减小)同样 的倍数。 un aus aus2...+bist bzis2 +.. ik=41,1+a24s2.+b,is1+b2is2+. 当激励只有一个时,则响应与激励成正比。 可加性(additivity property)
线性电路中,所有激励(独立源)都增大(或减小)同样 的倍数,则电路中响应(电压或电流)也增大(或减小)同样 的倍数。 当激励只有一个时,则响应与激励成正比。 可加性(additivity property)。 ... .. ... ... 2 ' 1 2 ' 2 1 ' 1 2 ' 1 1 1 2 2 1 1 2 2 = + + + + = + + + + k s S S S n s S S S i a u a u b i b i u a u a u b i b i 齐性原理(homogeneity property)