聊城大学：《电路分析》课程教学资源（PPT课件讲稿）第八章 相量法（1/2）

第8章 相量法 ●重点： 1.正弦量的表示、相位差 2.正弦量的相量表示 3.电路定理的相量形式

第8章 相量法 2. 正弦量的相量表示 3. 电路定理的相量形式 ⚫ 重点： 1. 正弦量的表示、相位差

8.1复数 复数4的表示形式 A=a+jb G=√-1为虚数单位 Im b b A=a+jb A=Aleio A=Ale=Al(cos0+jsine)=a+jb A=HA|e=HA|∠0

⚫ 复数A的表示形式 (j = − 1 为虚数单位) A b Re Im 0 a A=a+jb A b Re Im 0 a  |A| A A e A j a jb j =| | =| |(cos + sin ) = +  A = a + jb = =   A | A| e | A| j j A =| A| e 8.1 复数

两种表示法的关系： Im b [〔A=a+jb 直角坐标表示 LA=Alei=A 0 极坐标表示 1AVa2+62 a=Alcos0 b 或 e arctg b=Alsine 图解法 复数运算 Im (1)加减运算 采用代数形式 A=a+jb,A2=a2+jb2 Re 则A1±A2=(a1士2)十j(b1士b2)

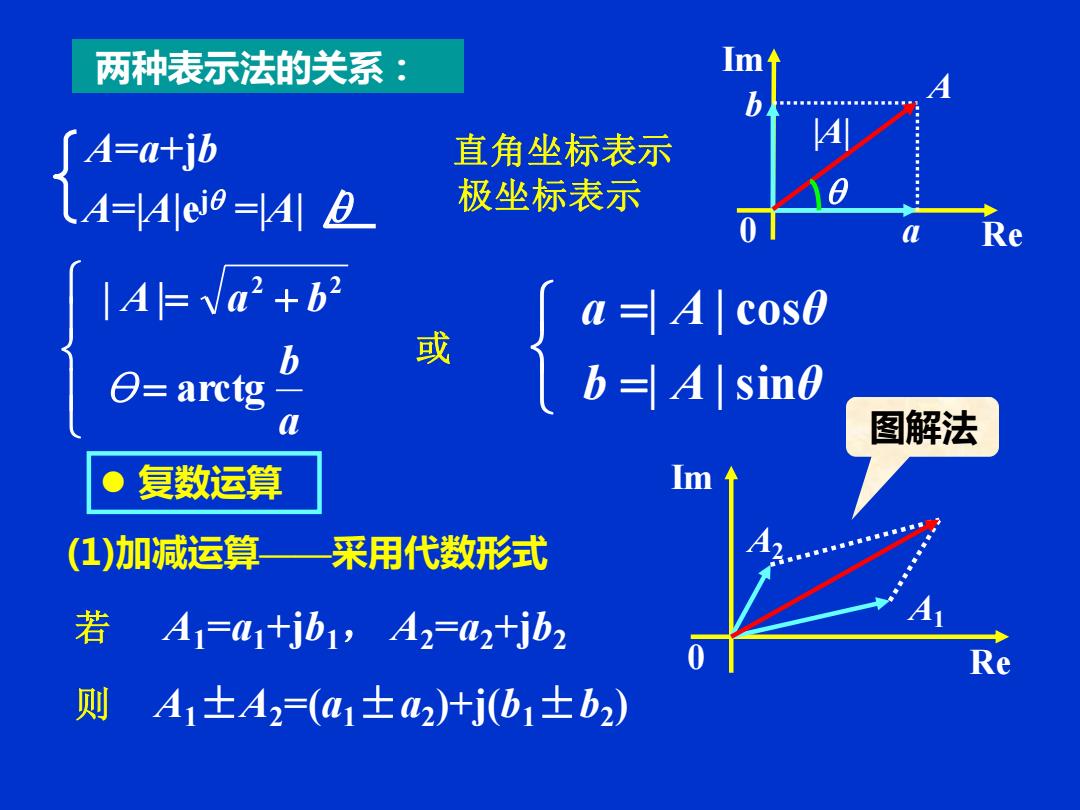
两种表示法的关系： A=a+jb A=|A|ej =|A|  直角坐标表示 极坐标表示      = = + a b θ A a b arctg | | 2 2 或    = = b A θ a | A | θ | |sin cos ⚫ 复数运算 则 A1±A2=(a1±a2 )+j(b1±b2 ) (1)加减运算——采用代数形式 若 A1=a1+jb1， A2=a2+jb2 A1 A2 Re Im 0 A b Re Im 0 a  |A| 图解法

(2)乘除运算 采用极坐标形式 若A=A1|/1,A2AlB2 则：A,A,=Ae8.Ae8=AA2e8+8. =A1A2∠8+0 乘法：模相乘，角相加。 A IAl∠011A,1e9 Aleio-) A |4,l∠021Aleo 1A21 除法：模相除，角相减。 1A2} 101-02 例1. 5∠47°+10∠-25°=？ 解 5∠47°+10∠-25°=(3.41+3.657)+(9.063-j4.226) =12.47-0.569=12.48∠-2.61°

(2) 乘除运算——采用极坐标形式 若 A1=|A1 |  1 ，A2=|A2 |  2 1 2 2 1 j( ) 2 1 j 2 2 j 1 2 2 1 1 2 1 | | | | e | | | | | | e | | e | | | | 1 2 1 θ θ A A A A A A A θ A θ A A θ θ θ θ = − = =   = − 除法：模相除，角相减。 例1. 乘法：模相乘，角相加。 则: 1 2 1 2 ( ) 1 2 1 2 1 2 1 2 1 2       =  +  =  = + A A A A A e A e A A e j j j 547 +10 − 25 = ?   547 +10− 25 = (3.41+ j3.657)+ (9.063− j4.226)   = 12.47 − j0.569  = 12.48 − 2.61 解

例2. 220∠35+17+9)(4+j6 20+j5 解 原式=180.2+126.2+ 9.24∠27.9°×7.211∠56.3 20.62∠14.04 =180.2+126.2+6.728∠70.16 =180.2+126.2+2.238+6.329 =182.5+132.5=225.5∠36 Im↑ A·ej0 (3)旋转因子： 复数ej0=cos0+isin0=1∠0 A·jB相当于A逆时针旋转一个角度0，而模不变。 故把ej称为旋转因子

例2. ? 20 j5 (17 j9) (4 j6) 220 35 = + + +  +  (3) 旋转因子： 复数 e j =cos +jsin =1∠ A• e j 相当于A逆时针旋转一个角度 ，而模不变。 故把 e j 称为旋转因子。 解 原式= 180.2+ j126.2    20.62 14.04 19.24 27.9 7.211 56.3     +  = 180.2+ j126.2+ 6.72870.16 = 180.2 + j126.2 + 2.238 + j6.329  = 182.5+ j132.5 = 225.536 A Re Im 0 A• e j 