
二、导数的定义 定义1.设函数y=f(x)在点x。的某邻域内有定义, 若 1m/(w-/xo)=1m D. Dy=f(x)-f(x) x®X0 x-xo Dx®OD Dx=x-xo 存在,则称函数(x)在点x处可导,并称此极限为 y=f(x)在点x的导数记作: y=;fx):】 v df(x) xx=xo dx x xo 即 y-o=fxo)=lim Dy x®ODX lim f(xo +Dx)-f(xo) lim f(xo +h)-f(xo) Dx®O Dx h®0 HIGH EDUCATION PRESS 返回 结
二、导数的定义 定义1 . 设函数 在点 存在, 并称此极限为 记作: 即 则称函数 若 的某邻域内有定义 , 在点 处可导, 在点 的导数. 机动 目录 上页 下页 返回 结束
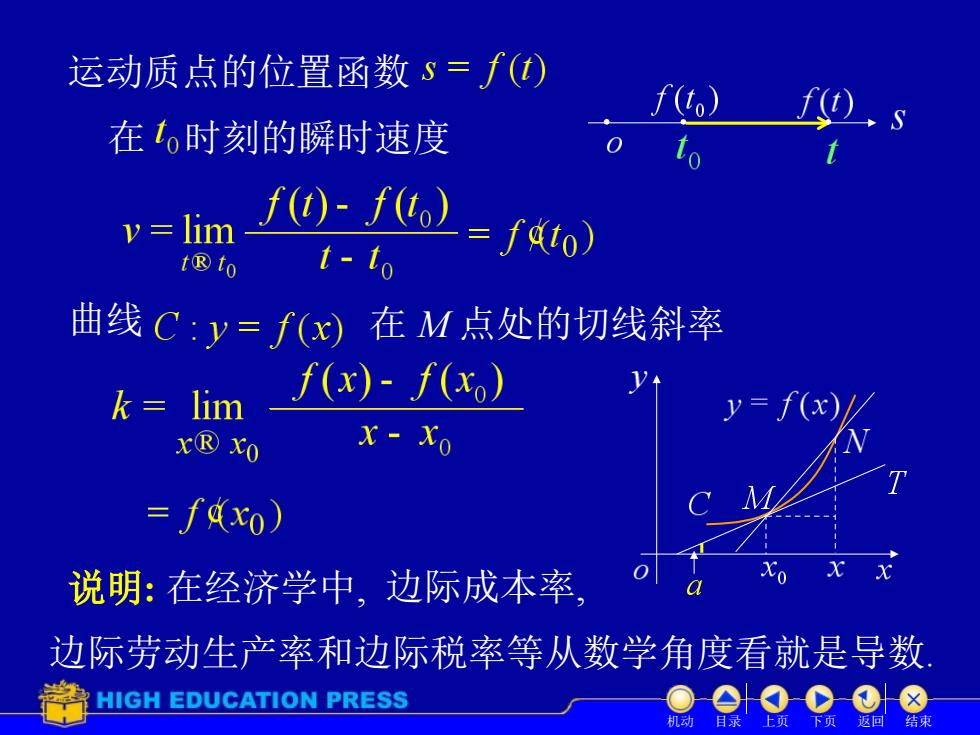
运动质点的位置函数s=f(t) f(t】 在1o时刻的瞬时速度 to y lim f0-f,)=fo) t®t0 t-to 曲线C:y=f(x) 在M点处的切线斜率 =lim- f(x)-f(x.) (x x®xo x-Xo =fdxo) 说明:在经济学中,边际成本率 边际劳动生产率和边际税率等从数学角度看就是导数 HIGH EDUCATION PRESS
运动质点的位置函数 在 时刻的瞬时速度 曲线 在 M 点处的切线斜率 说明: 在经济学中, 边际成本率, 边际劳动生产率和边际税率等从数学角度看就是导数. 机动 目录 上页 下页 返回 结束