《概率论与数理统计》课程教学课件（PPT讲稿）第07章 参数估计 7.5 正态总体均值与方差的区间估计

概率论与敖理统计 (2)σ2为未知 的置信度为1-o的没信区间X±，u- 推导过程如下： 由于区同X±小中含有未知参数o,不能 直接使用此区间 但因为S2是o2的无偏估计，可用S=V√S2替换σ

(2) ,  2为未知 , , / 2 直接使用此区间 由于区间 中含有未知参数 不 能          z n X , , 2 2 2 但因为S 是 的无偏估计 可用S  S 替换 的置信度为1的置信区间 ( 1) . / 2        t n  n S X  推导过程如下:

概率论与散理统外 又根据第六章定理三知 X=业~tn-1) S/√n 则P-a-是台-=1-a p以名wg.o-小-1e 于是得μ的置信度为1-α的置信区间 (x±kaa-

( 1) ( 1) 1 ,  / 2   / 2              t n  n S t n X n S 即 P X 于是得 的置信度为1 的置信区间 ( 1) . / 2        t n  n S X  ~ ( 1), /   t n S n X  又根据第六章定理三知 ( 1) 1 , / ( 1) / 2 / 2                   t n S n X 则 P t n

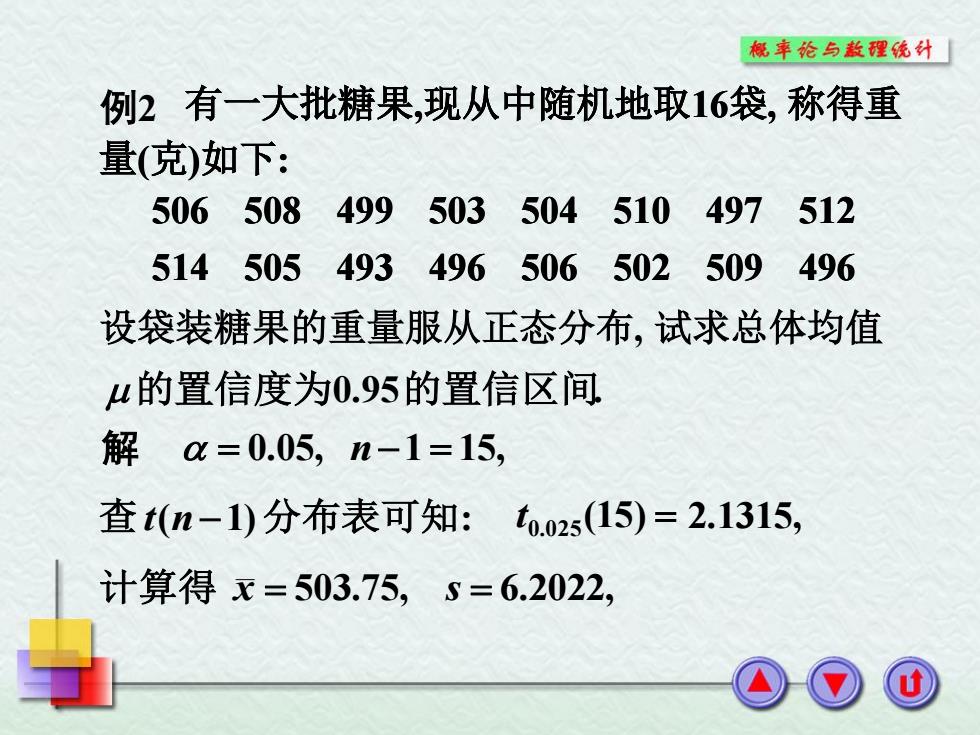
概率论与敖理统计】 例2有一大批糖果，现从中随机地取16袋，称得重 量（克）如下： 506508499 503504510497512 514505493496 506502509 496 设袋装糖果的重量服从正态分布，试求总体均值 μ的置信度为0.95的置信区间 解a=0.05,n-1=15, 查t(n-1)分布表可知：t.o25(15)=2.1315, 计算得x=503.75,s=6.2022

解 有一大批糖果,现从中随机地取16袋, 称得重 量(克)如下: 514 505 493 496 506 502 509 496 506 508 499 503 504 510 497 512 设袋装糖果的重量服从正态分布, 试求总体均值   0.05, n 1  15, 查 t(n 1)分布表可知: t 0.025(15)  计算得 x  503.75, s  6.2022, 的置信度为0.95的置信区间. 2.1315, 例2 有一大批糖果,现从中随机地取16袋, 称得重 量(克)如下: 514 505 493 496 506 502 509 496 506 508 499 503 504 510 497 512 有一大批糖果,现从中随机地取16袋, 称得重 量(克)如下: 514 505 493 496 506 502 509 496 506 508 499 503 504 510 497 512

概率论与数理统外「 得μ的置信度为95%的置信区间 503.75±6.20 2×2.1315 即 (500.4,507.10). √16 就是说估计袋装糖果重量的均值在500.4克与 507.1克之间，这个估计的可信程度为95%. 若依此区间内任一值作为4的近似值， 其误差不大于6.2022×2.1315×2=6.61（克. 16 这个误差的可信度为95%

得 的置信度为95%的置信区间         2.1315 16 6.2022 503.75 即 (500.4, 507.1). 就是说估计袋装糖果重量的均值在500.4克与 507.1克之间, 这个估计的可信程度为95%. 2.1315 2 6.61( ). 16 6.2022 其误差不大于    克 若依此区间内任一值作为的近似值, 这个误差的可信度为95%

概率论与敖理统外 2.方差σ2的置信区间 根据实际需要只介绍4未知的情况 方差σ的置信度为1-a的置信区间 (n-1)S2(n-1)S2 xa2(n-1)'22a2(n-1) 推导过程如下： 因为S2是σ2的无偏估计， 根据第六章第二节定理二知-S~m- 021

推导过程如下: , 因为S 2 是 2的无偏估计 ~ ( 1), ( 1) 2 2 2   n n S   根据第六章第二节定理二知 1 方差 2的置信度为 的置信区间. ( 1) ( 1) , ( 1) ( 1) 2 1 / 2 2 2 / 2 2              n n S n n S     根据实际需要, 只介绍 未知的情况. 2. 方差 2 的置信区间