
上§2.4一阶隐方程与参数表示 例侧223求方程y=(-x号 ⑨,2 dx 的通解。 解图令农=p,则原方程变为 d y=pp+ (2.40) 2 两边对x求导得p=2p dx +x或者写成 2-102p-)=0 由此即得 -1=0,或2p-x=0,由虫-1=0→p=x+c dx 代入(2.40)得通解 +cx+c2(1.41) 2 由2p-x=0,得,代2.41)得另一个解 (2.42) 4 考虑(2.41)与(2.42)之间的关系.解方程组 Fcx+c2 2 得交点坐标(c,c) A 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 例2.23 求方程 的通解. 2 2 ( ) 2 dy dy x y x dx dx = − + 解: 令 dy p dx = ,则原方程变为 = − + 2 2 (2.40) 2 x y p xp 两边对x求导得 2 dp dp p p p x x dx dx = − − + 或者写成 ( 1)(2 ) 0 dp p x dx − − = §2.4 一阶隐方程与参数表示 由此即得 1 0 2 0 dp p x dx − = − = ,或 , 代入(2.40)得通解 由 − = = + 1 0 dp p x c dx = + + 2 2 (1.41) 2 x y cx c 由 2 0 ,代入 2 (2.41)得另一个解 x p x p − = = ,得 = 2 (2.42) 4 x y 考虑(2.41)与(2.42)之间的关系. 解方程组 2 2 2 2 4 x y cx c x y = + + = 得交点坐标 2 ( ) c c
§2.4一阶隐方程与参数表示 即(2.41)中的每一条积分曲线都和(2.42)在(c,c相交.在交点(c,c2) 处,(2.41)和(2.42)的切线斜率都为(-c),这说明(2.41)中的每一条积分曲 线和(2.42)相切.这样的解称为奇解 曲线图象 3 (x2)4 Y轴 y=x2/2+cx+c2 y=x24 3 X轴 结束 上一贡同下一<2■ 目录 首页
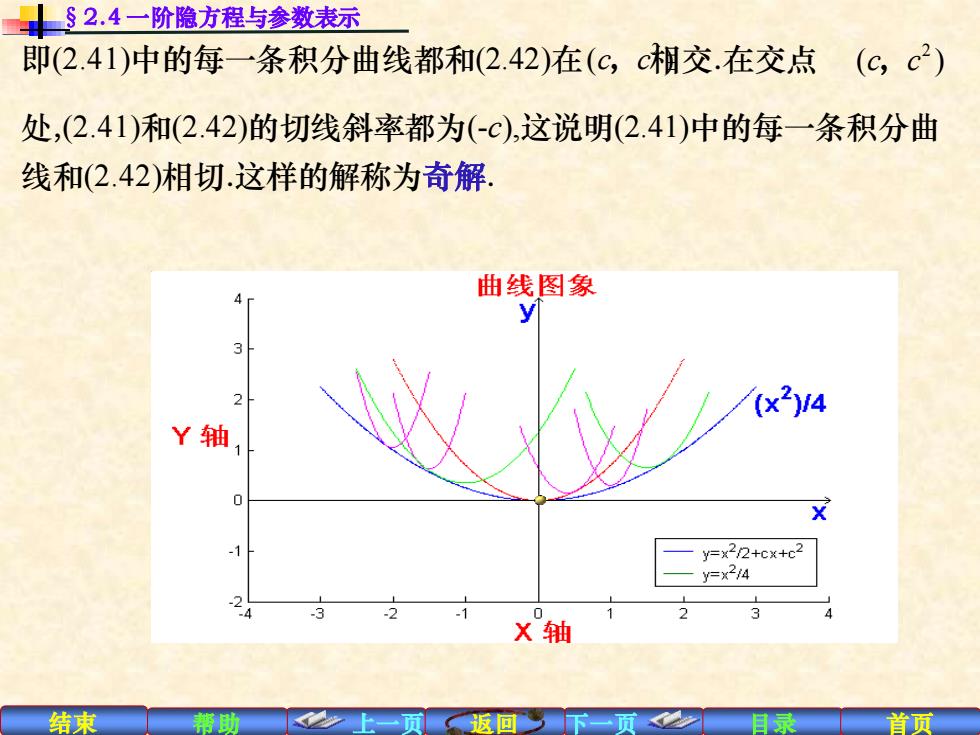
结束 帮助 上一页 返回 下一页 目录 首页 即(2.41)中的每一条积分曲线都和(2.42)在 相交.在交点 处,(2.41)和(2.42)的切线斜率都为(-c),这说明(2.41)中的每一条积分曲 线和(2.42)相切.这样的解称为奇解. §2.4 一阶隐方程与参数表示 2 ( ) c c , 2 ( ) c c , 4 2 x y = x y o