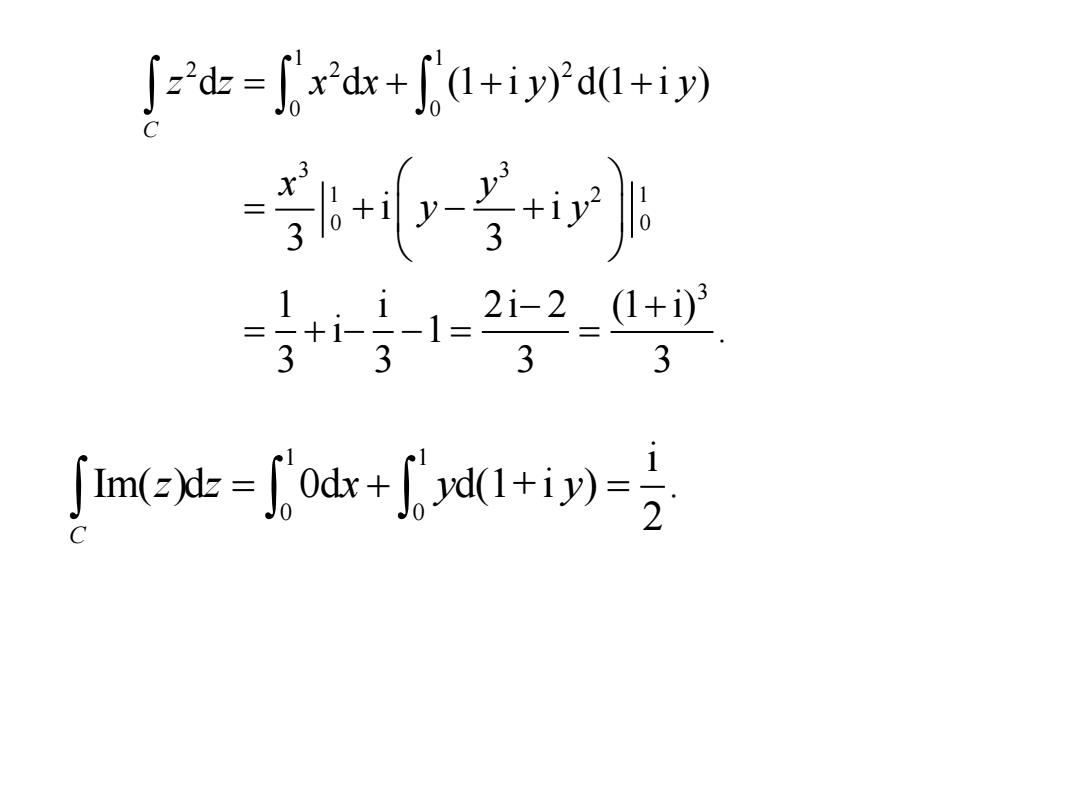
∫t=rdr+0+-iyd+-i) 号 1 3 i122- 3 33 met-odw+1+in=方
1 1 2 2 2 0 0 3 3 1 2 1 0 0 3 d d (1 i ) d(1 i ) i i 3 3 1 i 2i 2 (1 i) i 1 . 3 3 3 3 C z z x x y y x y y y = + + + = + − + − + = + − − = = 1 1 0 0 i Im( )d 0d d(1+i ) . 2 C z z x y y = + =

例3.2计算积分∮d,其中C为图3.2所示半圆环区域 的正向边界 解:积分路径可分为四段: 2i C1z=(-2≤t≤-1), C2=ei0,0从到0; C3z=(1≤t≤2): -2C1-1 1C32 C4=2e,0从0到元. ④d-Ed+c+d+d 2iedo
例3.2 计算积分 ,其中C为图3.2所示半圆环区域 的正向边界. d C z z z 解:积分路径可分为四段: C1 :z=t(-2≤ t ≤ -1); C2 :z= 从到0; C3 :z=t(1≤ t ≤ 2); C4 :z= 从0到. i e , i 2e , 1 2 3 4 1 0 2 i i π i i i i 2 π 1 0 d d d d d e 2e d ie d d 2ie d e 2e 2 4 4 1 1 . 3 3 3 C C C C C z z z z z z z z z z z z z z z t t t t t t − − − − = + + + = + + + = + + − =
例3.3计算积分本, dz,其中C为以为中心,为 半径的正向圆周,n为整数 解:曲线C的方程为:z=z。+re(0≤0≤2π) 2元 ireio y dz 2 20 2元 当n=0时1=i「d0=2πi 0 2元 当n≠0时,I=∫(cosn0-isn8d0=0 1 手 2πi,n=0, 。n≠0
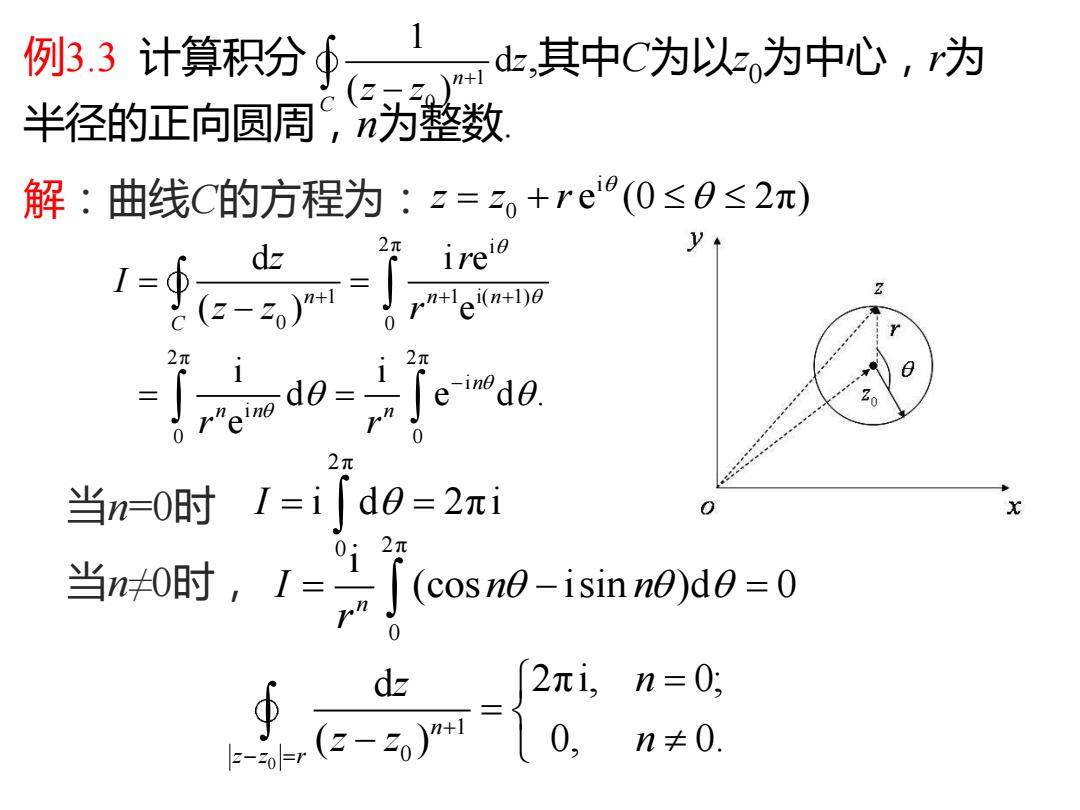
例3.3 计算积分 ,其中C为以z0为中心,r为 半径的正向圆周,n为整数. 1 0 1 d ( )n C z z z + − 解:曲线C的方程为: i 0 z z r e (0 2π) = + 2π i 1 1 i( 1) 0 0 2π 2π i i 0 0 d i e ( ) e i i d e d . e n n n C n n n n z r I z z r r r + + + − = = − = = 当n=0时 2π 0 I = = i d 2 πi 当n≠0时, 2π 0 i (cos isin )d 0 n I n n r = − = 0 1 0 d 2πi, 0; ( ) 0, 0. n z z r z n z z n + − = = = −

§3.2柯西-古萨定理及其推广 1.柯西-古萨(Cauchy-Goursat)定理 假设函数fz)=u+iv在单连通域D内处处解析,f(z) 在D内连续,u,对x,y的偏导数在D内连续设x+iy,C 为D内任一条简单闭曲线 ∫fe)d=∫udr-d+dr+ud 记G为C所围区域,由格林(Green)公式有 --〔盘 由于z)=u+iv在D内解析,所以u,v在D内处处都满足 柯西黎曼方程,即 8v Ov Ou Ox ay Ox ay
§3.2 柯西-古萨定理及其推广 1.柯西-古萨(Cauchy-Goursat)定理 假设函数f(z)=u+iv在单连通域D内处处解析,f'(z) 在D内连续, u,v对x,y的偏导数在D内连续.设z=x+iy,C 为D内任一条简单闭曲线. ( )d d d d d . C C C f z z u x v y i v x u y = − + + 记G为C所围区域,由格林(Green)公式有 d d d d , G C v u u x v y x y x y − = − − 由于f(z)=u+iv在D内解析,所以u,v在D内处处都满足 柯西-黎曼方程,即 , . u v v u x y x y = = −