
对于分段线性插值当数据点个数增加和相邻两(Xk+1,fk+1)点之间距离减Xk.t小时,线性插值就更精确。插值曲线在节点处不光滑不可导xx, =bX2 ...... Xkxi..... Xn-1a=xoXk+1是否存在一条连续光滑又不发生龙格现象”的插值曲线呢?
对于分段线性插值 . . 当数据点个数 增加和相邻两 点之间距离减 小时,线性插 值就更精确。 插值曲线 在节点处 不光滑, 不可导 是否存在一条连续光滑又不发生 “龙格现象”的插值曲线呢?
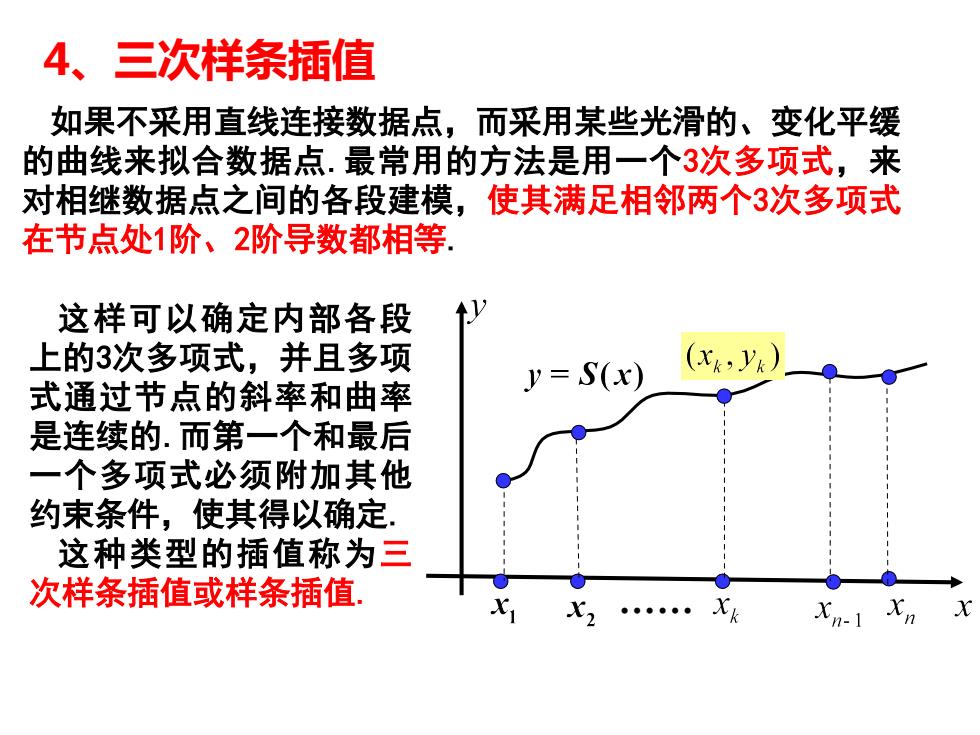
4三次样条插值如果不采用直线连接数据点,而采用某些光滑的、变化平缓的曲线来拟合数据点.最常用的方法是用一个3次多项式,来对相继数据点之间的各段建模,使其满足相邻两个3次多项式在节点处1阶、2阶导数都相等这样可以确定内部各段上的3次多项式,并且多项V= S(x式通过节点的斜率和曲率是连续的.而第一个和最后一个多项式必须附加其他约束条件,使其得以确定这种类型的插值称为三次样条插值或样条插值XXnxX,Axn-1
4、三次样条插值 如果不采用直线连接数据点,而采用某些光滑的、变化平缓 的曲线来拟合数据点.最常用的方法是用一个3次多项式,来 对相继数据点之间的各段建模,使其满足相邻两个3次多项式 在节点处1阶、2阶导数都相等. 这样可以确定内部各段 上的3次多项式,并且多项 式通过节点的斜率和曲率 是连续的.而第一个和最后 一个多项式必须附加其他 约束条件,使其得以确定. 这种类型的插值称为三 次样条插值或样条插值.

三次样条插值函数的建立对已知的n个数据点(xi,J),(x,,2),L,(x,,J,)设S(x)在每个子区间[x,,xi+i]上为一个3次多项式S,(x)=a,x3 + b,x2+c,x+d, (i=1,2,L ,n- 1)满足:S-(x)= S,(x,), Sg,(x,)= Sdx,),S(x,)= Sx,) (i= 2,3,L ,n- 1)在端点处满足:利用这些条件可以建立确定各段三次S,(x)= yi, S,(x,) = yn,多项式相应的大型线性方程组Sdx)=a1, S(x,) =b理论上可以证明此方程组有唯一解,从而确定n个三次多项式组成的分(a1,b,为端点的一阶导数值)段三次多项式函数S(x)Sax)= Sxn).三次样条插值的MATLAB命令:y0= spline(x, y, x0)其中x,y为已知数据点,yo为求得的插值函数在xo处的值
三次样条插值函数的建立 三次样条插值的MATLAB命令: y0= spline(x,y,x0) 其中x,y为已知数据点,y0为求得的插值函数在x0处的值。 利用这些条件可以建立确定各段三次 多项式相应的大型线性方程组. 理论上可以证明此方程组有唯一解, 从而确定由n个三次多项式组成的分 段三次多项式函数S(x)