
上游充通大兽 特殊复数 SHANGHAI JIAO TONG UNIVERSITY 如果mz=0,则z看成一个实数; 如果Imz不等于零,那么称z为一个虚数; 如果Imz不等于零,而Rez=0,则称z为一个纯虚数。 1.1.2复数的共轭运算与四则运算 2=x+y,2=x-y,x,y∈R (a1+ib,)±(a2+ib2)=(a1±a2)+(b±b2) (a1+ib,(a2+ib2)=(a,a2-b,b2)+i(a,b2+a2b) (a+ib) daz+bb.iabdbz (a2+b2)a+b a2+b2
特殊复数 如果 Imz=0,则z看成一个实数; 如果 Imz不等于零,那么称z为一个虚数; 如果 Imz不等于零,而Rez=0,则称z为一个纯虚数。 ( ) ( ) ( ) ( ) 1 1 2 2 1 2 1 2 a + ib ± a + ib = a ± a + i b ± b 1.1.2 复数的共轭运算与四则运算 ( )( ) ( ) ( ) 1 1 2 2 1 2 1 2 1 2 2 1 a + ib a + ib = a a − b b + i a b + a b 2 2 2 2 2 1 1 2 2 2 2 2 1 2 1 2 2 2 1 1 ( ) ( ) a b a b a b i a b a a b b a ib a ib + − + + + = + + z x iy z x iy x y R =+ =− ∈ ,

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 复数在四则运算这个代数结构下,构成一个数域 (对加、减、乘、除运算封闭,对加乘具有交换律、结合律 与分配律,加乘具有单位元与逆元),称为复数域, 记为C,复数域可以看成实数域的扩张
复数在四则运算这个代数结构下,构成一个数域 (对加、减、乘、除运算封闭,对加乘具有交换律、结合律 与分配律,加乘具有单位元与逆元),称为复数域, 记为C, 复数域可以看成实数域的扩张

上游充通大 1.1.3 复数的几何意义 SHANGHAI JIAO TONG UNIVERSITY 一个复数z=x+y本质上由一对有序实数对(x,y) 唯一确定。作映射: 1-1对应 C→R2:z=x+iyS(x,y) (双射) 复数域C也可以理解成平面RxR,我们称C为 复平面. 平面上横坐标轴称为实轴,纵坐标轴称为虚 轴. 注:C中“数”与复平面上“点”看作等同
1.1.3 复数的几何意义 复数域C 也可以理解成平面RxR,我们称C为 复平面. 平面上横坐标轴称为实轴,纵坐标轴称为虚 轴. : ( , ) 2 C → R z = x + iy x y 一个复数 z=x+iy 本质上由一对有序实数对(x, y) 唯一确定。作映射: 1-1对应 (双射) 注:C中“数”与复平面上“点”看作等同
上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY 复数的向量表示 (x,y) C上向量与复数z=x+业也构成 一一 对应的关系,则复数可以等同于平面 中的向量等价类(在平移关系下)。向量 的长度称为复数的模,定义为 |z=√x2+y2= Z与正实轴之间的夹角称为复数的辐角,定义为: Argz=0+2kπcR,K为整数. 注1:z=0时辐角无意义。z卡0时Agz为无穷多值函数,辐角 的多值性是很多复变函数多值性的根源. 注2:两个复数相等的充要条件:它们模相等,辐角相差2kπ
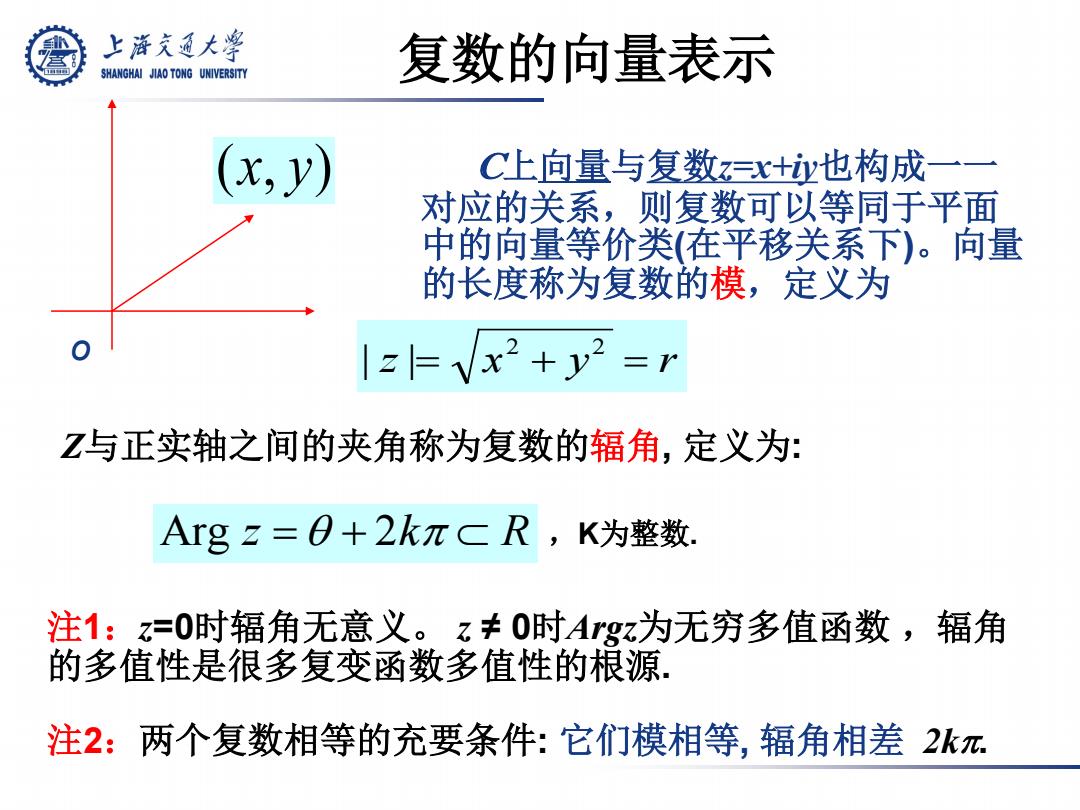
复数的向量表示 C上向量与复数z=x+iy也构成一一 对应的关系,则复数可以等同于平面 中的向量等价类(在平移关系下)。向量 的长度称为复数的模,定义为 z = x + y = r 2 2 | | Z与正实轴之间的夹角称为复数的辐角, 定义为: Arg 2 z kR =+ ⊂ θ π 注1:z=0时辐角无意义。 z ≠ 0时Argz为无穷多值函数 ,辐角 的多值性是很多复变函数多值性的根源. (x, y) ,K为整数. o 注2:两个复数相等的充要条件: 它们模相等, 辐角相差 2kπ

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 辐角主值argz:取Argz的一个属于 (一π,π]之间的特殊值. arctan上 x>0, X π 21 x=0,y>0, arg z =arctan +, x<0,y≥0, x arctan y -π, x<0,y<0, X π x=0,y<0 2 Argz=argz+2kπ,k∈Z
辐角主值argz:取Argz的一个属于 ( ] −π ,π 之间的特殊值. − = < − < < + < ≥ = > > = , 0, 0. 2 arctan , 0, 0, arctan , 0, 0, , 0, 0, 2 arctan , 0, arg x y x y x y x y x y x y x x y z π π π π Arg arg 2 , z z kk =+ ∈ π Z